6 Capítulo Sobreajuste y el desarrollo de técnicas para resolverlo

“La simplicidad es la sofisticación suprema.” - Leonardo da Vinci

Los modelos de deep learning tienen una poderosa capacidad para representar funciones complejas a través de numerosos parámetros. Sin embargo, esta capacidad a veces puede ser un doble filo. Cuando el modelo se ajusta excesivamente a los datos de entrenamiento, se produce el fenómeno de sobreajuste (overfitting), donde el rendimiento de predicción en nuevos datos disminuye.

Desde que el algoritmo de retropropagación fue revisado en 1986, el sobreajuste ha sido un desafío constante para los investigadores de deep learning. Inicialmente, se abordaba reduciendo el tamaño del modelo o aumentando la cantidad de datos de entrenamiento. Sin embargo, estos métodos tenían limitaciones, ya que restringían la capacidad expresiva del modelo o presentaban dificultades en la recopilación de datos. La aparición de AlexNet en 2012 marcó el inicio de una nueva era para el deep learning, pero también resaltó la gravedad del problema de sobreajuste. AlexNet tenía muchos más parámetros que los modelos anteriores, lo que aumentaba el riesgo de sobreajuste. A medida que la escala de los modelos de deep learning creció exponencialmente, el problema de sobreajuste se convirtió en un tema central de investigación.

En este capítulo, exploraremos la esencia del sobreajuste y examinaremos las diversas técnicas que han evolucionado para abordarlo. Al igual que los exploradores que mapean territorios desconocidos, los investigadores de deep learning han buscado constantemente nuevas formas para superar el desafío del sobreajuste.

6.1 Comprensión del Sobreajuste

El sobreajuste fue mencionado por primera vez en las obras de William Hopkins en 1670, pero en su sentido moderno comenzó con una referencia en Quarterly Review of Biology en 1935: “Hacer un análisis multivariante de 6 variables con solo 13 observaciones parece un sobreajuste”. A partir de la década de 1950, se empezó a estudiar sistemáticamente en estadística, y fue particularmente importante en el contexto del análisis de series temporales en el artículo “Tests of Fit in Time Series” de 1952.

El problema de sobreajuste en deep learning tomó un nuevo rumbo con la aparición de AlexNet en 2012. AlexNet era una red neuronal a gran escala con aproximadamente 60 millones de parámetros, lo que representaba un salto significativo respecto a los modelos anteriores. A medida que la escala de los modelos de deep learning creció exponencialmente, el problema de sobreajuste se volvió más grave. Por ejemplo, los modernos modelos de lenguaje a gran escala (LLM) tienen billones de parámetros, lo que hace que prevenir el sobreajuste sea una tarea crucial en el diseño del modelo.

Para abordar estos desafíos, se propusieron soluciones innovadoras como dropout (2014) y batch normalization (2015), y recientemente se han investigado métodos más sofisticados para detectar y prevenir el sobreajuste utilizando historiales de entrenamiento (2024). En particular, en modelos a gran escala, se utilizan estrategias diversas que van desde técnicas tradicionales como early stopping hasta ensembles learning y data augmentation.

Vamos a entender intuitivamente el fenómeno de sobreajuste a través de un ejemplo simple. Aplicaremos polinomios (polynomial) de diferentes grados (degree) a datos de una función seno (sine) con ruido.

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

import numpy as np
import seaborn as sns

# Noisy sin graph
def real_func(x):
    y = np.sin(x) + np.random.uniform(-0.2, 0.2, len(x))
    return y

# Create x data from 40 to 320 degrees.  Use a step value to avoid making it too dense.
x = np.array([np.pi/180 * i for i in range(40, 320, 4)])

y = real_func(x)


import seaborn as sns

sns.scatterplot(x=x, y=y, label='real function')

# Plot with 1st, 3rd, and 21th degree polynomials.  
for deg in [1, 3, 21]:  
# Get the coefficients for the corresponding degree using polyfit, and create the estimated function using poly1d.
    params = np.polyfit(x, y, deg) # Get the parameter values
    # print(f" {deg} params = {params}")
    p = np.poly1d(params) # Get the line function
    sns.lineplot(x=x, y=p(x), color=f"C{deg}", label=f"deg = {deg}")

The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

/tmp/ipykernel_1362795/2136320363.py:25: RankWarning: Polyfit may be poorly conditioned
  params = np.polyfit(x, y, deg) # Get the parameter values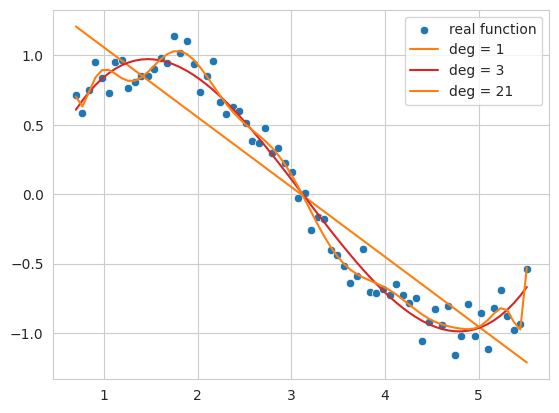

El siguiente código genera datos de una función senoidal con ruido y ajusta (fitting) estos datos usando polinomios de 1º, 3º y 21º grado.

• Función de 1º grado (deg = 1): no sigue la tendencia general de los datos y se muestra en forma de línea simple. Esto demuestra un estado de subajuste (underfitting) donde el modelo no expresa suficientemente la complejidad de los datos.

• Función de 3º grado (deg = 3): captura relativamente bien el patrón básico de los datos, mostrando una curva suave que no se ve demasiado afectada por el ruido.

• Función de 21º grado (deg = 21): sigue excesivamente incluso el ruido en los datos de entrenamiento, mostrando un estado de sobreajuste (overfitting) donde el modelo está demasiado optimizado para los datos de entrenamiento.

Así, si la complejidad del modelo (en este caso, el grado del polinomio) es demasiado baja, ocurre subajuste; si es demasiado alta, ocurre sobreajuste. Lo que buscamos finalmente es un modelo que se generalice bien no solo a los datos de entrenamiento sino también a nuevos datos, es decir, la función de aproximación más cercana a la función senoidal real.

El sobreajuste ocurre cuando la complejidad del modelo (capacidad) es relativamente alta en comparación con la cantidad de datos de entrenamiento. Las redes neuronales tienen un gran número de parámetros y una alta capacidad de expresión, por lo que son particularmente vulnerables al sobreajuste. El sobreajuste también puede ocurrir cuando los datos de entrenamiento son insuficientes o contienen mucho ruido. El sobreajuste se caracteriza por las siguientes características:

• La pérdida (loss) en los datos de entrenamiento sigue disminuyendo.
• La pérdida en los datos de validación disminuye inicialmente, pero a partir de un cierto punto comienza a aumentar.
• Esto es debido a que el modelo aprende incluso el ruido y los detalles finos de los datos de entrenamiento, especializándose excesivamente en ellos.

En resumen, un modelo sobreajustado muestra un alto rendimiento en los datos de entrenamiento pero un bajo rendimiento predictivo en nuevos datos reales. Para prevenir este sobreajuste, examinaremos detalladamente técnicas como la regularización L1/L2, el dropout y la normalización por lotes.

6.2 Técnicas de regularización

Desafío: ¿Cuál es un método para mejorar el rendimiento de generalización mientras se controla eficazmente la complejidad del modelo?

Angustia del investigador: Reducir el tamaño del modelo para evitar el sobreajuste puede limitar su capacidad de expresión, y simplemente aumentar los datos de entrenamiento no siempre es posible. Se necesitaba un método que imponga restricciones a la estructura del modelo o al proceso de aprendizaje para prevenir una optimización excesiva de los datos de entrenamiento y mejorar el rendimiento predictivo en nuevos datos.

6.2.1 Regularización L1, L2

Entre las técnicas de regularización (regularization) más utilizadas en redes neuronales se encuentran la regularización L1 y L2. L1 se refiere a Lasso, mientras que L2 se refiere a Ridge (regresión lineal).

También conocidas como regresión Ridge y regresión Lasso, cada una introduce un término de penalización para limitar el movimiento de los parámetros. Las diferencias características entre ambos métodos se pueden resumir en la siguiente tabla.

Característica	Regresión Ridge (Ridge Regression)	Regresión Lasso (Lasso Regression)
Tipo de penalización	Aplica una penalización L2. El término de penalización es el producto de la suma de los cuadrados de los parámetros por un valor alfa.	Aplica una penalización L1. El término de penalización es el producto de la suma de los valores absolutos de los parámetros por un valor alfa.
Efecto en los parámetros	Suprime los parámetros con grandes valores, llevándolos a ser cercanos a cero, pero no exactamente cero	Cuando el valor de alfa es grande, puede hacer que algunos parámetros sean exactamente cero, creando un modelo más simple
Efecto general	Todos los parámetros se conservan. Por lo tanto, incluso los parámetros con menor impacto permanecen.	Solo quedan los parámetros relevantes, lo que confiere propiedades selectivas y permite explicar modelos complejos de manera más simple.
Características de optimización	Menos sensible a valores ideales en comparación con Lasso.	Es sensible a valores ideales debido al término de penalización absoluto.

La expresión matemática es la siguiente.

• Función objetivo de Ridge (Ridge Regression Objective Function)

  “Función objetivo modificada de Ridge” = (función de regresión lineal no modificada) + \(\alpha \cdot \sum (\text{parámetro})^2\)

  \(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2\)

  Aquí, \(\beta\) es el vector de parámetros (pesos) que se desea encontrar. \(\alpha \sum_{j} \beta_{j}^2\) se conoce como término de penalización o término de regularización. \(\alpha\) es un hiperparámetro que ajusta la magnitud del término de regularización. La fórmula para encontrar los parámetros es:

  \(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} \beta_{j}^2 \right)\)

• Función objetivo de Lasso (Lasso Regression Objective Function)

  “Función objetivo modificada de Lasso” = (función de regresión lineal no modificada) + $ || $

  \(f_{\beta} = \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_{j}|\) \(\beta = \underset{\beta}{\operatorname{argmin}} \left( \sum_{i=1}^{M} (y_i - \hat{y}_i)^2 + \alpha \sum_{j} |\beta_j| \right)\)

El uso de la penalización de la suma de cuadrados de los parámetros, conocido como L2, es comúnmente llamado atenuación de peso (weight decay) en redes neuronales. Vamos a examinar cómo difiere el uso de regresión Ridge (L2) del regresión lineal simple utilizando un modelo implementado en sklearn. Para esto, es necesario aumentar la dimensionalidad de los datos de entrada x según el grado. Usaremos una función utilitaria simple para crear estos datos.

def get_x_powered(x, p=1):
    size = len(x)

    # The shape of the created x will be (data size, degree)
    new_x = np.zeros((size, p))

    for s in range(len(x)): # Iterate over data size
        for d in range(1, p+1): # Iterate over degrees
            new_x[s][d-1] = x[s]**d # Raise x to the power of the degree.

    return new_x


# Let's take a quick look at how it works.
deg = 3
x = np.array([np.pi/180 * i for i in range(20, 35, 5)])
y = real_func(x)  # real_func는 이전 코드에 정의되어 있다고 가정

print(f"x = {x}")
new_x = get_x_powered(x, p=deg)

print(f"new_x = {new_x}")

x = [0.34906585 0.43633231 0.52359878]
new_x = [[0.34906585 0.12184697 0.04253262]
 [0.43633231 0.19038589 0.08307151]
 [0.52359878 0.27415568 0.14354758]]

Debido a que es de tercer orden, los valores de \(x\) aumentan a \(x^2, x^3\). Por ejemplo, 0.3490, 0.1218 (el cuadrado de 0.3490), 0.04253 (el cubo de 0.3490) son ejemplos de esto. Si fuera de décimo orden, se generarían datos hasta \(x^{10}\). El valor alfa del término de penalización puede tomar valores desde 0 hasta infinito. Cuanto mayor sea el valor alfa, mayor será la intensidad de la regularización. Fijaremos el grado en 13 y compararemos las funciones de regresión lineal y de regresión ridge mientras variamos el valor alfa.

import numpy as np
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# Create a noisy sine wave (increased noise)
def real_func(x):
    return np.sin(x) + np.random.normal(0, 0.4, len(x))  # Increased noise

# Create x data (narrower range)
x = np.array([np.pi / 180 * i for i in range(40, 280, 8)])  # Narrower range, larger step

y = real_func(x)

# Degree of the polynomial
deg = 10

# List of alpha values to compare (adjusted)
alpha_list = [0.0, 0.1, 10]  # Adjusted alpha values
cols = len(alpha_list)

fig, axes_list = plt.subplots(1, cols, figsize=(20, 5))  # Adjusted figure size

for i, alpha in enumerate(alpha_list):
    axes = axes_list[i]

    # Plot the original data
    sns.scatterplot(ax=axes, x=x, y=y, label='real function', s=50)  # Increased marker size

    # Plot linear regression
    params = np.polyfit(x, y, deg)
    p = np.poly1d(params)
    sns.lineplot(ax=axes, x=x, y=p(x), label=f"LR deg = {deg}")

    # Ridge regression (using Pipeline, solver='auto')
    model = make_pipeline(PolynomialFeatures(degree=deg), Ridge(alpha=alpha, solver='auto'))
    model.fit(x.reshape(-1, 1), y)  # Reshape x for pipeline
    y_pred = model.predict(x.reshape(-1, 1)) # Reshape x for prediction
    sns.lineplot(ax=axes, x=x, y=y_pred, label=f"Ridge alpha={alpha:0.1e} deg={deg}")

    axes.set_title(f"Alpha = {alpha:0.1e}")
    axes.set_ylim(-1.5, 1.5)  # Limit y-axis range
    axes.legend()

plt.tight_layout()
plt.show()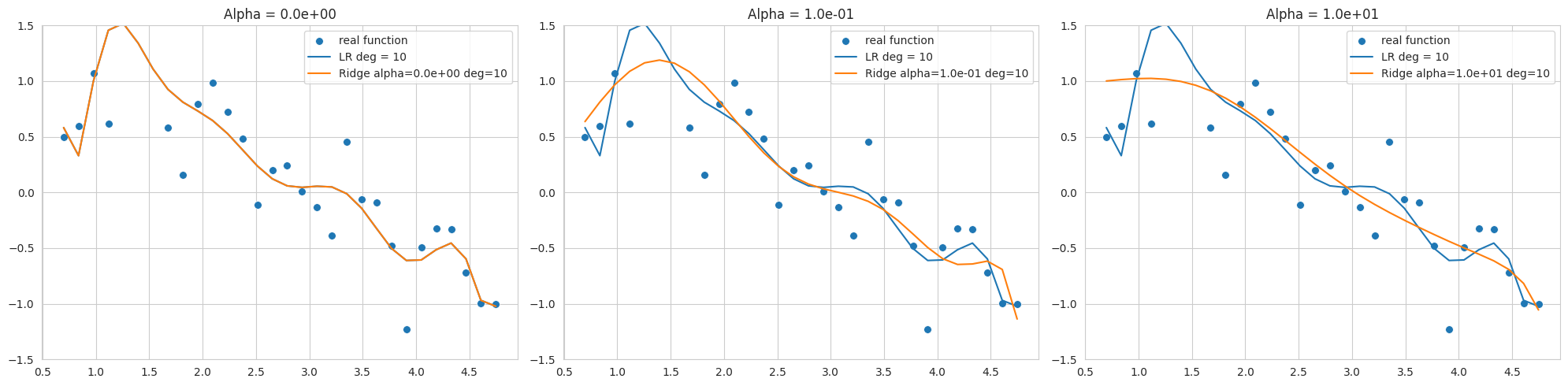

El gráfico muestra el resultado de ajustar datos de una función seno con ruido utilizando un polinomio de grado 10, mostrando los resultados de la regresión Ridge con diferentes valores de alpha (fuerza de regularización). Dado que el rango de datos es estrecho y el ruido es alto, es fácil producir overfitting incluso a bajo grado.

• Alpha = 0.0: La regresión Ridge se vuelve igual a la regresión lineal de mínimos cuadrados ordinarios, y un polinomio de grado 10 sigue el ruido en los datos de entrenamiento, mostrando una forma de overfitting muy ondulada.
• Alpha = 0.1: Se aplica una regularización débil, lo que reduce las ondulaciones en comparación con alpha=0, pero aún es sensible al ruido y dista de la función seno.
• Alpha = 10: Con una fuerte regularización, la curva se vuelve mucho más suave, representando bien la tendencia general de los datos (la función seno). Esto demuestra que la regularización L2 (regresión Ridge) controla eficazmente el overfitting.

Seleccionar un valor adecuado de alpha permite controlar la complejidad del modelo y mejorar su rendimiento en generalización. La regularización L2 es útil para estabilizar el modelo al hacer que los pesos sean cercanos a 0.

El modelo sklearn.linear_model.Ridge puede utilizar diferentes métodos de optimización según el solver seleccionado. En particular, cuando el rango de datos es estrecho y hay mucho ruido, como en este ejemplo, los solvers 'svd' o 'cholesky' pueden ser más estables, por lo que se debe tener cuidado al elegir el solver (en el código se especifica 'cholesky').

6.2.2 Aplicación de L1 y L2 regularización en PyTorch

PyTorch y Keras difieren en la forma de implementar la regularización L1 y L2. Keras permite agregar términos de regularización directamente a cada capa (kernel_regularizer, bias_regularizer).

6.2.2 Aplicación de L1 y L2 regulación en PyTorch

PyTorch y Keras tienen diferencias en la forma de implementar la regulación L1 y L2. Keras soporta agregar términos de regulación directamente a cada capa (como kernel_regularizer, bias_regularizer).

# In Keras, you can specify regularization when declaring a layer.
keras.layers.Dense(64, activation='relu',
                    kernel_regularizer=regularizers.l2(0.01),
                    input_shape=(784,))

Mientras tanto, PyTorch aplica la regularización L2 configurando la decadencia de peso (weight decay) en el optimizador (optimizer), y la regularización L1 generalmente se implementa a través de una función de pérdida personalizada.

import torch.nn as nn
import torch

def custom_loss(outputs, targets, model, lambda_l1=0.01, lambda_l2=0.01,):
    mse_loss = nn.MSELoss()(outputs, targets)
    
    l1_loss = 0.
    l2_loss = 0.
    for param in model.parameters():
        l1_loss += torch.sum(torch.abs(param)) # Take the absolute value of the parameters.
        l2_loss += torch.sum(param ** 2)  # Square the parameters.
    
    total_loss = mse_loss + lambda_l1 * l1_loss + lambda_l2 * l2_loss # Add L1 and L2 penalty terms to the loss.
    return total_loss

# Example usage within a training loop (not runnable as is)
# for inputs, targets in dataloader:
#     # ... (rest of the training loop)
#     loss = custom_loss(outputs, targets, model)
#     loss.backward()
    # ... (rest of the training loop)

Como en el ejemplo anterior, se puede definir una función custom_loss para aplicar tanto la regularización L1 como L2. Sin embargo, generalmente se configura el weight_decay, que corresponde a la regularización L2, en el optimizador. Sin embargo, los optimizadores Adam y SGD implementan el peso de decadencia ligeramente diferente a la regularización L2. La regularización L2 tradicional añade un término cuadrático de parámetros a la función de pérdida.

\(L_{n+1} = L_{n} + \frac{ \lambda }{2} \sum w^2\)

La derivada de esto con respecto a los parámetros es la siguiente:

\(\frac{\partial L_{n+1}}{\partial w} = \frac{\partial L_{n}}{\partial w} +\lambda w\)

SGD y Adam implementan esto añadiendo directamente el término \(\lambda w\) al gradiente. El código de SGD en chapter_05/optimizers/ es el siguiente.

if self.weight_decay != 0:
    grad = grad.add(p, alpha=self.weight_decay)

Este método no produce exactamente el mismo efecto que agregar un término de regularización L2 a la función de pérdida cuando se combina con momentum o tasas de aprendizaje adaptativas.

Separación del Decaimiento de Peso en AdamW (Decoupled Weight Decay)

En el artículo “Fixing Weight Decay Regularization in Adam” publicado en ICLR 2017 (https://arxiv.org/abs/1711.05101), se destacó que la atenuación de pesos en el optimizador Adam funciona de manera diferente a la regularización L2, y se propuso el optimizador AdamW para corregir este problema. En AdamW, el decaimiento de peso se separa del ajuste de gradiente y se aplica directamente durante la etapa de actualización de parámetros. El código está en el mismo basic.py.

# PyTorch AdamW weght decay
if weight_decay != 0:
    param.data.mul_(1 - lr * weight_decay)

AdamW multiplica los valores de los parámetros por 1 - lr * weight_decay.

• Decaimiento de pesos en el Adam original: En la etapa de actualización de gradientes, el término de decaimiento de pesos (\(\lambda w\)) se considera junto con la tasa de aprendizaje (\(lr\)) y otros términos de ajuste de gradiente (por ejemplo, momentum). Esto puede hacer que el efecto del decaimiento de pesos varíe según la tasa de aprendizaje y la configuración de otros hiperparámetros.
• Decaimiento de pesos en AdamW: El decaimiento de pesos se aplica por separado en la etapa de actualización de parámetros, lo que lo hace menos dependiente de la tasa de aprendizaje u otros hiperparámetros. Es decir, el efecto del decaimiento de pesos es más predecible y consistente.

En conclusión, el enfoque de AdamW se acerca más a una implementación precisa de la regularización L2. Llamar al decaimiento de pesos en SGD, Adam como regularización L2 se debe a razones históricas y efectos similares, pero estrictamente es más preciso verlo como una técnica de regularización separada, y AdamW clarifica esta diferencia para ofrecer un mejor rendimiento.

6.2.3 Análisis del efecto de la regularización en el plano de pérdida

Para comprender visualmente el impacto de la regularización L1 y L2 en el aprendizaje del modelo, utilizaremos la técnica de visualización del plano de pérdida (loss surface) introducida en el Capítulo 4. Compararemos los cambios en el plano de pérdida entre el caso sin regularización y el caso con regularización L2, observando cómo varía la posición de la solución óptima según la intensidad de la regularización (weight_decay).

import sys

from dldna.chapter_05.visualization.loss_surface import xy_perturb_loss,  hessian_eigenvectors, visualize_loss_surface 
from dldna.chapter_04.utils.data import get_dataset, get_device   
from dldna.chapter_04.utils.metrics import load_model  

import torch
import torch.nn as nn
import numpy as np
import torch.utils.data as data_utils
from torch.utils.data import  DataLoader


device = get_device()  # Get the device (CPU or CUDA)
train_dataset, test_dataset = get_dataset()  # Load the datasets.  

act_name = "ReLU"
model_file = f"SimpleNetwork-{act_name}.pth"

small_dataset = data_utils.Subset(test_dataset, torch.arange(0, 256))  # Use a subset of the test dataset
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)  # Create a data loader
loss_func = nn.CrossEntropyLoss()  # Define the loss function

# Load the trained model.
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU") # 4장의 load_model 사용
trained_model = trained_model.to(device)  # Move the model to the device

top_n = 2  # Number of top eigenvalues/eigenvectors to compute
top_eigenvalues, top_eigenvectors =  hessian_eigenvectors(model=trained_model, loss_func=loss_func, data_loader=data_loader, top_n=top_n, is_cuda=True)  # 5장의 함수 사용

d_min ,d_max, d_num = -1, 1, 50  # Define the range and number of points for the grid
lambda1, lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32), np.linspace(d_min, d_max, d_num).astype(np.float32)  # Create the grid of lambda values
x, y, z = xy_perturb_loss(model=trained_model, top_eigenvectors=top_eigenvectors, data_loader=data_loader, loss_func=loss_func, lambda1=lambda1, lambda2=lambda2, device=device) # 5장의 함수 사용

Se crea una función de aproximación con xy_perturb_loss y luego se vuelven a introducir (x, y) en esa función de aproximación para calcular un nuevo valor de z. La razón por la que se hace esto es porque si se trazan las líneas de contorno utilizando los valores obtenidos con xy_perturb_loss, como se muestra en el Capítulo 5, el punto mínimo puede variar ligeramente, lo que causa que el optimizador converja a un punto ligeramente diferente. Ahora, en lugar de mostrar toda la trayectoria por la que fluye el optimizador, solo se comparan los puntos más bajos finales mientras se aumenta el valor de amortiguación weight_decay.

import torch
import numpy as np
import torch.nn as nn
import torch.optim as optim  # Import optim
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader, Subset

# 5장, 4장 함수들 import
from dldna.chapter_05.visualization.loss_surface import (
    hessian_eigenvectors,
    xy_perturb_loss,
    visualize_loss_surface
)
from dldna.chapter_04.utils.data import get_dataset, get_device
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_05.visualization.gaussian_loss_surface import (
    get_opt_params,
    train_loss_surface,
    gaussian_func # gaussian_func 추가.
)


device = get_device()
_, test_dataset = get_dataset(dataset="FashionMNIST") 
small_dataset = Subset(test_dataset, torch.arange(0, 256))
data_loader = DataLoader(small_dataset, batch_size=256, shuffle=True)
loss_func = nn.CrossEntropyLoss()

act_name = "ReLU" # Tanh로 실험하려면 이 부분을 변경
model_file = f"SimpleNetwork-{act_name}.pth"
trained_model, _ = load_model(model_file=model_file, path="./tmp/opts/ReLU") 
trained_model = trained_model.to(device)

top_n = 2
top_eigenvalues, top_eigenvectors = hessian_eigenvectors(
    model=trained_model,
    loss_func=loss_func,
    data_loader=data_loader,
    top_n=top_n,
    is_cuda=True
)

d_min, d_max, d_num = -1, 1, 30 # 5장의 30을 사용
lambda1 = np.linspace(d_min, d_max, d_num).astype(np.float32)
lambda2 = np.linspace(d_min, d_max, d_num).astype(np.float32)

x, y, z = xy_perturb_loss(
    model=trained_model,
    top_eigenvectors=top_eigenvectors,
    data_loader=data_loader,
    loss_func=loss_func,
    lambda1=lambda1,
    lambda2=lambda2,
    device=device # device 추가
)


# --- Optimization and Visualization ---

# Find the parameters that best fit the data.
popt, _, offset = get_opt_params(x, y, z)  # offset 사용

print(f"Optimal parameters: {popt}")

# Get a new z using the optimized surface function (Gaussian).
# No need for global g_offset, we can use the returned offset.
z_fitted = gaussian_func((x, y), *popt,offset) # offset을 더해야 함.


data = [(x, y, z_fitted)]  # Use z_fitted

axes = visualize_loss_surface(data, act_name=act_name, color="C0", size=6, levels=80, alpha=0.7, plot_3d=False)
ax = axes[0]

# Train with different weight decays and plot trajectories.
for n, weight_decay in enumerate([0.0, 6.0, 10.0, 18.0, 20.0]):
# for n, weight_decay in enumerate([0.0]):  # For faster testing
    points_sgd_m = train_loss_surface(
        lambda params: optim.SGD(params, lr=0.1, momentum=0.7, weight_decay=weight_decay),
        [d_min, d_max],
        200,
        (*popt, offset) # unpack popt and offset
    )
    ax.plot(
        points_sgd_m[-1, 0],
        points_sgd_m[-1, 1],
        color=f"C{n}",
        marker="o",
        markersize=10,
        zorder=2,
        label=f"wd={weight_decay:0.1f}"
    )
    ax.ticklabel_format(axis='both', style='scientific', scilimits=(0, 0))

plt.legend()
plt.show()

Function parameters = [ 4.59165436  0.34582255 -0.03204057 -1.09810435  1.54530407]
Optimal parameters: [ 4.59165436  0.34582255 -0.03204057 -1.09810435  1.54530407]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.8065, 0.9251]
SGD: Iter=200 loss=1.9090 w=[0.3458, -0.0320]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[-0.2065, 0.3251]
SGD: Iter=200 loss=1.9952 w=[0.1327, -0.0077]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.1935, -0.0749]
SGD: Iter=200 loss=2.0293 w=[0.0935, -0.0051]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[0.9935, -0.8749]
SGD: Iter=200 loss=2.0641 w=[0.0587, -0.0030]

train_loss_surface: SGD
SGD: Iter=1 loss=4.7671 w=[1.1935, -1.0749]
SGD: Iter=200 loss=2.0694 w=[0.0537, -0.0027]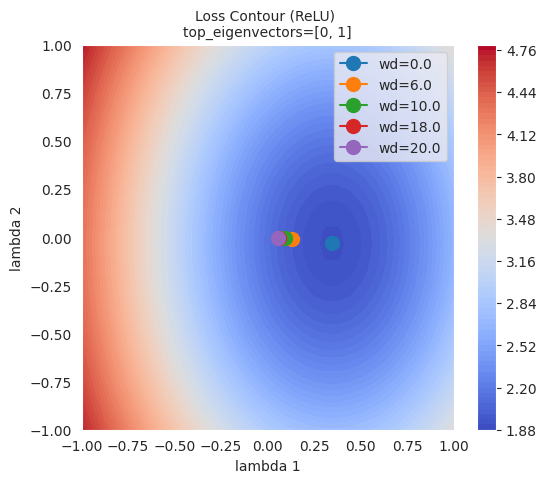

Como se puede ver en la figura, cuanto mayor es la regulación L2 (weight decay), más lejos del punto mínimo de la función de pérdida llega el optimizador. Esto se debe a que la regulación L2 previene que los pesos sean demasiado grandes, lo cual ayuda a evitar el sobreajuste del modelo.

La regulación L1 crea un modelo disperso (sparse model) al hacer que algunos pesos sean 0. Es útil cuando se desea reducir la complejidad del modelo y eliminar características innecesarias. Por otro lado, la regulación L1 no reduce los pesos completamente a 0, sino que mantiene todos los pesos pequeños. La regulación L2 generalmente muestra una convergencia más estable y, debido a que disminuye gradualmente los pesos, también se conoce como ‘regulación suave’.

La regulación L1 y la regulación L2 se aplican de manera diferente según las características del problema, los datos y el objetivo del modelo. Aunque generalmente se usa más la regulación L2, es aconsejable probar ambas regularizaciones en diferentes situaciones y ver cuál ofrece un mejor rendimiento. Además, también se puede considerar la regularización Elastic Net, que combina las regularizaciones L1 y L2.

Haga clic para ver el contenido (deep dive: Regularización Elastic Net - la armonía entre L1 y L2)

Regulación Elastic Net - Armonía entre L1 y L2

Elastic Net es un método de regularización que combina la regulación L1 y la regulación L2. Tomando las ventajas de cada regulación y compensando sus desventajas, se puede crear un modelo más flexible y efectivo.

Núcleo:

• Regulación L1 (Lasso): Limita la suma de los valores absolutos de los pesos. Crea un modelo disperso (sparse) al hacer que algunos pesos sean exactamente 0. Tiene un efecto de selección de características, eliminando características innecesarias y simplificando el modelo.
• Regulación L2 (Ridge): Limita la suma de los cuadrados de los pesos. Mantiene todos los pesos pequeños para prevenir el sobreajuste del modelo. La convergencia es estable y reduce suavemente los pesos.
• Elastic Net: Aplica simultáneamente la regulación L1 y L2. Se pueden obtener los efectos de ambas regulaciones.

Fórmula:

La función de costo de Elastic Net se expresa de la siguiente manera.

\(Cost = Loss + \lambda_1 \sum_{i} |w_i| + \lambda_2 \sum_{i} (w_i)^2\)

• Loss: La función de pérdida del modelo original (ej: MSE, Cross-Entropy)
• λ₁: Hiperparámetro que controla la intensidad de la regulación L1
• λ₂: Hiperparámetro que controla la intensidad de la regulación L2
• wᵢ: Los pesos del modelo

Ventajas:

• Selección de características + prevención de sobreajuste: Se pueden obtener los efectos de selección de características de la regulación L1 y la prevención de sobreajuste de la regulación L2.
• Tratamiento de características altamente correlacionadas: La regulación L1 tiende a seleccionar una sola característica de un conjunto de características altamente correlacionadas y hacer que las demás sean 0. Elastic Net alivia este problema a través de la regulación L2, tendiendo a seleccionar o eliminar juntas las características altamente correlacionadas.
• Flexibilidad: Se puede ajustar el λ₁ y el λ₂ para equilibrar la proporción de la regulación L1 y L2. Si λ₁=0, se obtiene la regulación L2 (Ridge); si λ₂=0, se obtiene la regulación L1 (Lasso).

Desventajas:

• Ajuste de hiperparámetros: Se deben ajustar dos hiperparámetros, λ₁ y λ₂, lo que puede ser más complejo que ajustar solo uno para la regulación L1 o L2.
• Costo computacional: Al calcular simultáneamente la regulación L1 y L2, el costo computacional puede aumentar ligeramente (no es un gran problema en el aprendizaje automático moderno).

Cuándo aplicar:

• Cuando se tienen muchas características y se espera que solo algunas sean importantes (cuando se necesita selección de características)
• Cuando las características están altamente correlacionadas
• Cuando no está claro si la regulación L1 o L2 es mejor (cuando se desea probar ambas)
• Para prevenir el sobreajuste mientras se crea un modelo que sea disperso en cierto grado

Resumen: Elastic Net es un método de regularización poderoso que combina las ventajas de L1 y L2. Aunque requiere ajuste de hiperparámetros, puede mostrar un buen rendimiento en una variedad de problemas.

6.3 Dropout (드롭아웃)

6.3.1 Principio del dropout

El dropout es uno de los métodos de regularización más poderosos para prevenir el sobreajuste en las redes neuronales. Durante el proceso de aprendizaje, se desactivan (dropout) aleatoriamente algunas neuronas para evitar que ciertas neuronas o combinaciones de neuronas dependan excesivamente de los datos de entrenamiento. Esto tiene un efecto similar al aprendizaje en conjunto, donde varias personas aprenden diferentes partes y luego colaboran para resolver el problema. Se induce a cada neurona a aprender características importantes de manera independiente, lo que mejora el rendimiento general del modelo. Generalmente se aplica a las capas completamente conectadas (fully connected layer), y la tasa de desactivación se establece entre 20% y 50%. El dropout solo se aplica durante el entrenamiento, mientras que en la inferencia se utilizan todas las neuronas.

6.3.2 Implementación del dropout en PyTorch

En PyTorch, el dropout puede implementarse de manera simple de la siguiente manera.

import torch.nn as nn

class Dropout(nn.Module):
    def __init__(self, dropout_rate):
        super(Dropout, self).__init__()
        self.dropout_rate = dropout_rate

    def forward(self, x):
        if self.training:
            mask = torch.bernoulli(torch.ones_like(x) * (1 - self.dropout_rate)) / (1 - self.dropout_rate)
            return x * mask
        else:
            return x

# Usage example.  Drops out 0.5 (50%).
dropout = Dropout(dropout_rate=0.5)

# Example input data
inputs = torch.randn(1000, 100)

# Forward pass (during training)
dropout.train()
outputs_train = dropout(inputs)

# Forward pass (during inference)
dropout.eval()
outputs_test = dropout(inputs)

print("Input shape:", inputs.shape)
print("Training output shape:", outputs_train.shape)
print("Test output shape", outputs_test.shape)
print("Dropout rate (should be close to 0.5):", 1 - torch.count_nonzero(outputs_train) / outputs_train.numel())

Input shape: torch.Size([1000, 100])
Training output shape: torch.Size([1000, 100])
Test output shape torch.Size([1000, 100])
Dropout rate (should be close to 0.5): tensor(0.4997)

La implementación es muy simple. Se multiplica el valor de mask por el tensor de entrada para desactivar una proporción determinada de neuronas. La capa de dropout no tiene parámetros aprendibles separados, simplemente convierte en 0 aleatoriamente parte de la entrada. En redes neuronales prácticas, las capas de dropout se insertan entre otras capas (por ejemplo, capas lineales, capas de convolución) para su uso. El dropout elimina aleatoriamente neuronas durante el entrenamiento, pero utiliza todas las neuronas durante la inferencia. Para ajustar la escala de los valores de salida durante el entrenamiento y la inferencia, se utiliza el método de dropout invertido. El dropout invertido realiza un escalado anticipado dividiendo por (1 - dropout_rate) durante el entrenamiento, lo que permite usar directamente los valores sin operaciones adicionales durante la inferencia. De esta manera, se puede obtener un efecto similar al del aprendizaje conjunto durante la inferencia, es decir, promediando varios sub-redes parciales (sub-networks), mientras también se mejora la eficiencia computacional.

Vamos a examinar qué tan efectivo es el dropout utilizando gráficos con datos simples. El código fuente está en chapter_06/plot_dropout.py, y aunque es importante, no lo presentaremos aquí por brevedad. Los comentarios detallados hacen que ver el código sea sencillo. Al graficar los resultados, se puede observar que el modelo con dropout (azul) tiene una precisión de prueba significativamente mayor.

from dldna.chapter_06.plot_dropout import plot_dropout_effect

plot_dropout_effect()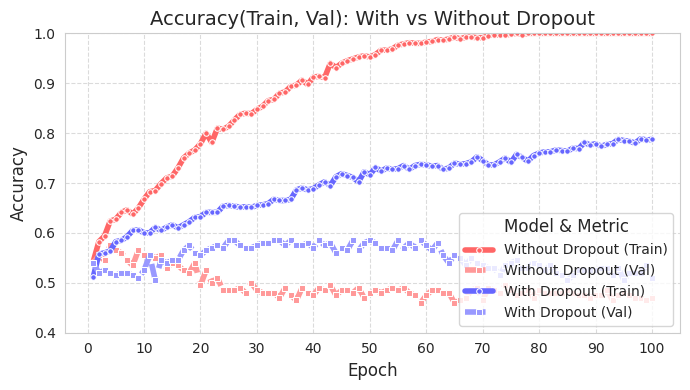

La precisión de entrenamiento del modelo con dropout (With Dropout) es menor que la del modelo sin dropout (Without Dropout), pero la precisión de validación es mayor. Esto significa que el dropout reduce el sobreajuste a los datos de entrenamiento y mejora el rendimiento de generalización del modelo.

6.4 Normalización por lotes (batch normalization)

6.4.1 Concepto y efectos de la normalización por lotes

La normalización por lotes es un método que, además de actuar como regularización, aumenta la estabilidad de los datos durante el entrenamiento. La normalización por lotes fue propuesta por primera vez en 2015 por Ioffe y Szegedy en su artículo [referencia 2]. En el aprendizaje profundo, ocurre un fenómeno denominado cambio interno de covariables (internal covariate shift), donde la distribución de los valores de activación cambia a medida que los datos pasan por cada capa. Esto ralentiza el entrenamiento y hace que el modelo sea inestable (se necesitan más pasos de cálculo debido al cambio en la distribución). Este problema se agrava especialmente cuando hay más capas. La normalización por lotes mitiga este problema normalizando los datos a nivel de mini lote.

La idea central de la normalización por lotes es normalizar los datos a nivel de mini lote. El siguiente código ilustra esto de manera sencilla.

# Calculate the mean and variance of the mini-batch
batch_mean = x.mean(dim=0)
batch_var = x.var(dim=0, unbiased=False)

# Perform normalization
x_norm = (x - batch_mean) / torch.sqrt(batch_var + epsilon)

# Apply scale and shift parameters
y = gamma * x_norm + beta

Generalmente, la normalización por lotes utiliza la varianza y la media de los datos dentro de un solo lote de entrenamiento para ajustar adecuadamente la distribución de todos los datos. Primero se realiza la normalización y luego se aplican parámetros de escala y desplazamiento en cierto grado. El gamma anterior es el parámetro de escala y beta es el parámetro de desplazamiento. Es conveniente pensar simplemente en \(y = ax + b\). Epsilon, utilizado durante la normalización, es un valor constante muy pequeño (1e-5 o 1e-7) común en análisis numérico. Se utiliza para garantizar la estabilidad numérica. La normalización por lotes proporciona los siguientes efectos adicionales:

• Aumento de la velocidad de aprendizaje: Estabiliza la distribución de los valores de activación de cada capa, mitigando el problema del desvanecimiento/explotación del gradiente y permitiendo el uso de tasas de aprendizaje más altas.
• Reducción de la dependencia de la inicialización: Reduce la sensibilidad a la inicialización de pesos, facilitando el inicio del proceso de aprendizaje.
• Efecto regularizador: Al calcular estadísticas por lotes, tiene un efecto similar al de agregar ruido, lo que ayuda a prevenir el sobreajuste (overfitting). Su eficacia se mejora cuando se usa junto con Dropout.

Vamos a crear datos aleatorios con dos características y comparar gráficamente los casos en los que se aplica la normalización pura y los que incluyen parámetros de escala y desplazamiento. A través de la visualización, será fácil comprender el significado numérico de la normalización en un lote de entrenamiento.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# Generate data
np.random.seed(42)
x = np.random.rand(50, 2) * 10

# Batch normalization (including scaling parameters)
def batch_normalize(x, epsilon=1e-5, gamma=1.0, beta=0.0):
    mean = x.mean(axis=0)
    var = x.var(axis=0)
    x_norm = (x - mean) / np.sqrt(var + epsilon)
    x_scaled = gamma * x_norm + beta
    return x_norm, mean, x_scaled

# Perform normalization (gamma=1.0, beta=0.0 is pure normalization)
x_norm, mean, x_norm_scaled = batch_normalize(x, gamma=1.0, beta=0.0)
# Perform normalization and scaling (apply gamma=2.0, beta=1.0)
_, _, x_scaled = batch_normalize(x, gamma=2.0, beta=1.0)

# Set Seaborn style
sns.set_style("whitegrid")
sns.set_context("notebook", font_scale=1.2)

# Visualization
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(18, 5))

# Original data
sns.scatterplot(x=x[:, 0], y=x[:, 1], ax=ax1, color='royalblue', alpha=0.7)
ax1.scatter(mean[0], mean[1], color='red', marker='*', s=200, label='Mean')
ax1.set(title='Original Data',
        xlabel='Feature 1',
        ylabel='Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax1.legend()

# After normalization (gamma=1, beta=0)
sns.scatterplot(x=x_norm[:, 0], y=x_norm[:, 1], ax=ax2, color='crimson', alpha=0.7)
ax2.scatter(0, 0, color='blue', marker='*', s=200, label='Mean (0,0)')
ax2.axhline(y=0, color='k', linestyle='--', alpha=0.3)
ax2.axvline(x=0, color='k', linestyle='--', alpha=0.3)
ax2.set(title='After Normalization (γ=1, β=0)',
        xlabel='Normalized Feature 1',
        ylabel='Normalized Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax2.legend()

# After scaling and shifting (gamma=2, beta=1)
sns.scatterplot(x=x_scaled[:, 0], y=x_scaled[:, 1], ax=ax3, color='green', alpha=0.7)
ax3.scatter(1, 1, color='purple', marker='*', s=200, label='New Mean')
ax3.axhline(y=1, color='k', linestyle='--', alpha=0.3)
ax3.axvline(x=1, color='k', linestyle='--', alpha=0.3)
ax3.set(title='After Scale & Shift (γ=2, β=1)',
        xlabel='Scaled Feature 1',
        ylabel='Scaled Feature 2',
        xlim=(-2, 12),
        ylim=(-2, 12))
ax3.legend()

plt.tight_layout()
plt.show()

# Print statistics
print("\nOriginal Data Statistics:")
print(f"Mean: {mean}")
print(f"Variance: {x.var(axis=0)}")

print("\nNormalized Data Statistics (γ=1, β=0):")
print(f"Mean: {x_norm.mean(axis=0)}")
print(f"Variance: {x_norm.var(axis=0)}")

print("\nScaled Data Statistics (γ=2, β=1):")
print(f"Mean: {x_scaled.mean(axis=0)}")
print(f"Variance: {x_scaled.var(axis=0)}")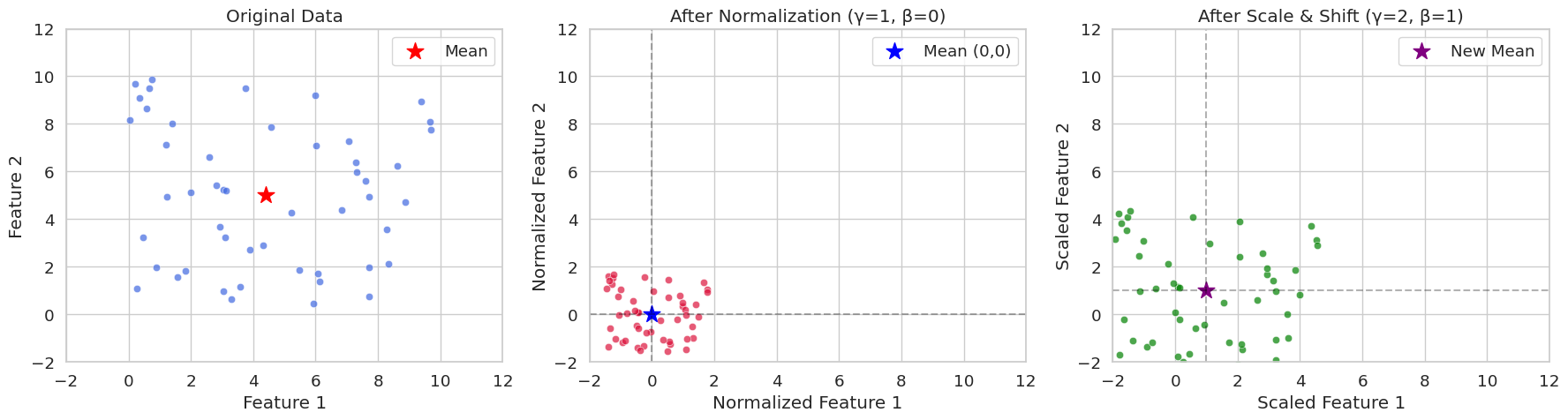

Original Data Statistics:
Mean: [4.40716778 4.99644709]
Variance: [8.89458134 8.45478364]

Normalized Data Statistics (γ=1, β=0):
Mean: [-2.70894418e-16 -3.59712260e-16]
Variance: [0.99999888 0.99999882]

Scaled Data Statistics (γ=2, β=1):
Mean: [1. 1.]
Variance: [3.9999955  3.99999527]

En seed(42) es común ver el valor de inicialización aleatoria establecido en 42. Esta es una práctica habitual entre los programadores, aunque se puede usar cualquier otro número. El 42 es un número que aparece en la novela “La guía del autoestopista galáctico” de Douglas Adams como “la respuesta a la vida, el universo y todo lo demás”. Por esta razón, se utiliza comúnmente en el código de ejemplo y entre los programadores.

6.4.2 Implementación de la normalización por lotes en PyTorch

En PyTorch, la implementación generalmente implica insertar una capa de normalización por lotes en las capas de la red neuronal. A continuación se muestra un ejemplo.

import torch.nn as nn

class SimpleNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.network = nn.Sequential(
            nn.Linear(784, 256),
            nn.BatchNorm1d(256),  # 배치 정규화 층
            nn.ReLU(),
            nn.Linear(256, 10)
        )
    
    def forward(self, x):
        return self.network(x)

En PyTorch, la implementación de la normalización por lotes simplificada a partir del código fuente original es como sigue. Al igual que en el capítulo anterior, esto se ha implementado de manera concisa con fines educativos.

import torch
import torch.nn as nn

class BatchNorm1d(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super().__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum

        # Trainable parameters
        self.gamma = nn.Parameter(torch.ones(num_features))  # scale
        self.beta = nn.Parameter(torch.zeros(num_features))  # shift

        # Running statistics to be tracked
        self.register_buffer('running_mean', torch.zeros(num_features))
        self.register_buffer('running_var', torch.ones(num_features))

    def forward(self, x):
        if self.training:
            # Calculate mini-batch statistics
            batch_mean = x.mean(dim=0)  # Mean per channel
            batch_var = x.var(dim=0, unbiased=False)  # Variance per channel

            # Update running statistics (important)
            self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
            self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var

            # Normalize
            x_norm = (x - batch_mean) / torch.sqrt(batch_var + self.eps)

        else:
            # During inference, use the stored statistics
            x_norm = (x - self.running_mean) / torch.sqrt(self.running_var + self.eps)

        # Apply scale and shift
        return self.gamma * x_norm + self.beta

La parte más diferente con respecto a la implementación básica es la actualización de las estadísticas durante la ejecución. Durante el entrenamiento, se acumula el movimiento de las estadísticas del mini-lote (media y varianza) para finalmente poder conocer la media y varianza totales. Para seguir este movimiento, se utiliza una media móvil exponencial (Exponential Moving Average) con un momento (valor predeterminado 0.1). Al utilizar esta media y varianza obtenidas durante el entrenamiento en la inferencia, se aplica una varianza y desviación precisas a los datos de inferencia, garantizando la consistencia entre el aprendizaje y la inferencia.

Por supuesto, esta implementación es muy simplificada para fines educativos. La ubicación del código de referencia es (https://github.com/pytorch/pytorch/blob/main/torch/nn/modules/batchnorm.py). La implementación real de BatchNorm1d es mucho más compleja. Esto se debe a que, en frameworks como PyTorch y TensorFlow, además de la lógica básica, incluyen diversas optimizaciones como CUDA, optimización de gradientes, manejo de diferentes configuraciones, integración con C/C++, entre otros.

Haga clic para ver el contenido (análisis detallado de la derivación matemática y el proceso de retropropagación de la normalización por lotes)

Derivación de la fórmula y análisis detallado del proceso de retropropagación de la normalización por lotes

La normalización por lotes (Batch Normalization, BN) se ha establecido como una de las técnicas clave en el aprendizaje de modelos de deep learning desde que fue propuesta por Ioffe & Szegedy en 2015. BN normaliza las entradas de cada capa para acelerar la velocidad de aprendizaje, mitigar los problemas de desvanecimiento/explotación del gradiente y proporcionar cierto efecto de regularización. En este deep dive, examinaremos detalladamente el proceso de propagación hacia adelante y retropropagación de BN, y analizaremos sus efectos matemáticamente.

Derivación de la fórmula de propagación hacia adelante (Forward Pass) de la normalización por lotes

La normalización por lotes se realiza en unidades de mini-lotes (mini-batches). Si consideramos el tamaño del mini-lote como \(B\) y la dimensión de las características (features) como \(D\), los datos de entrada del mini-lote se pueden representar como una matriz \(\mathbf{X}\) de tamaño \(B \times D\). BN se realiza independientemente para cada dimensión de las características, por lo que consideraremos solo las operaciones para una dimensión de característica en particular.

1. Cálculo de la media del mini-lote:

   \(\mu_B = \frac{1}{B} \sum_{i=1}^{B} x_i\)

   Aquí, \(x_i\) representa el valor de la característica correspondiente al \(i\)-ésimo ejemplo en el mini-lote.

2. Cálculo de la varianza del mini-lote:

   \(\sigma_B^2 = \frac{1}{B} \sum_{i=1}^{B} (x_i - \mu_B)^2\)

3. Normalización:

   \(\hat{x_i} = \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\)

   Aquí, \(\epsilon\) es una pequeña constante para evitar que el denominador sea cero.

4. Escalado y desplazamiento (Scale and Shift):

   \(y_i = \gamma \hat{x_i} + \beta\)

   Aquí, \(\gamma\) y \(\beta\) son parámetros aprendibles que se encargan del escalado y el desplazamiento, respectivamente. Estos parámetros juegan un papel en restaurar la capacidad de representación de los datos normalizados.

Derivación de la fórmula de retropropagación (Backward Pass) de la normalización por lotes - incluyendo gráfico de cálculo

La retropropagación de la normalización por lotes implica calcular las derivadas de la función de pérdida con respecto a cada parámetro utilizando la regla de la cadena. Este proceso se puede visualizar a través de un gráfico de cálculo, que se muestra a continuación. (Aquí se representa brevemente mediante ASCII art)

     x_i   -->   [-]   -->   [/]   -->   [*]   -->   [+]   -->   y_i
      |          ^          ^          ^          ^
      |          |          |          |          |
      |          |          |          |          +---> beta
      |          |          |          +---> gamma
      |          |          +---> sqrt(...) + epsilon
      |          +---> mu_B, sigma_B^2

• \(x_i\): entrada
• \([-]\): resta (\(x_i - \mu_B\))
• \([/]\): división (\((x_i - \mu_B) / \sqrt{\sigma_B^2 + \epsilon}\))
• \([*]\): multiplicación (\(\gamma \hat{x_i}\))
• \([+]\): suma (\(\gamma \hat{x_i} + \beta\))
• \(y_i\): salida
• \(\mu_B\): media
• \(\sigma_B^2\): varianza
• \(\epsilon\): pequeño número para evitar que el denominador sea cero
• \(\gamma, \beta\): parámetros de aprendizaje Ahora, calculemos el backpropagation paso a paso. Denotemos la función de pérdida como \(\mathcal{L}\) y supongamos que se nos da \(\frac{\partial \mathcal{L}}{\partial y_i}\).

1. Cálculo de \(\frac{\partial \mathcal{L}}{\partial \beta}\) y \(\frac{\partial \mathcal{L}}{\partial \gamma}\):

   \(\frac{\partial \mathcal{L}}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \beta} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i}\)

   \(\frac{\partial \mathcal{L}}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \gamma} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial y_i} \cdot \hat{x_i}\)

2. Cálculo de \(\frac{\partial \mathcal{L}}{\partial \hat{x_i}}\):

   \(\frac{\partial \mathcal{L}}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \frac{\partial y_i}{\partial \hat{x_i}} = \frac{\partial \mathcal{L}}{\partial y_i} \cdot \gamma\)

3. Cálculo de \(\frac{\partial \mathcal{L}}{\partial \sigma_B^2}\):

   \(\frac{\partial \mathcal{L}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \sigma_B^2} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot (x_i - \mu_B) \cdot (-\frac{1}{2})(\sigma_B^2 + \epsilon)^{-3/2}\)

4. Cálculo de \(\frac{\partial \mathcal{L}}{\partial \mu_B}\):

   \(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial \mu_B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot (-2)\frac{1}{B}\sum_{i=1}^B (x_i-\mu_B)\)

   Dado que \(\sum_{i=1}^B (x_i - \mu_B) = 0\) \(\frac{\partial \mathcal{L}}{\partial \mu_B} = \sum_{i=1}^{B} \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{-1}{\sqrt{\sigma_B^2 + \epsilon}}\)

5. Cálculo de \(\frac{\partial \mathcal{L}}{\partial x_i}\):

   \(\frac{\partial \mathcal{L}}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{\partial \hat{x_i}}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{\partial \mu_B}{\partial x_i} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{\partial \sigma_B^2}{\partial x_i} = \frac{\partial \mathcal{L}}{\partial \hat{x_i}} \cdot \frac{1}{\sqrt{\sigma_B^2 + \epsilon}} + \frac{\partial \mathcal{L}}{\partial \mu_B} \cdot \frac{1}{B} + \frac{\partial \mathcal{L}}{\partial \sigma_B^2} \cdot \frac{2}{B}(x_i - \mu_B)\)

Explicación de cómo la normalización por lotes mitiga el problema de desvanecimiento/estallido del gradiente

La normalización por lotes evita que las entradas a las funciones de activación se sesguen hacia valores extremos al normalizar las entradas en cada capa. Esto ayuda a mitigar el problema de desvanecimiento/estallido del gradiente, que ocurre en funciones de activación como la sigmoide o tanh.

• Problema de desvanecimiento del gradiente: Cuando las entradas a una función de activación son muy grandes o pequeñas, la pendiente de esa función se acerca a 0, lo que provoca que el gradiente se desvanezca durante la retropropagación. La normalización por lotes mantiene las entradas de la función de activación en un rango adecuado al normalizarlas con media 0 y varianza 1, mitigando así el problema de desvanecimiento del gradiente.

• Problema de estallido del gradiente: Cuando las entradas a una función de activación son muy grandes, la pendiente se vuelve extremadamente grande. La normalización por lotes limita el rango de entrada, mitigando también el problema de estallido del gradiente.

Cálculo y uso del promedio móvil (running mean, running variance) durante la inferencia en la normalización por lotes

Durante el entrenamiento, la normalización por lotes calcula la media y varianza para cada mini-lote. Sin embargo, durante la inferencia se necesitan estimaciones de la media y varianza del conjunto completo de datos de entrenamiento. Para esto, la normalización por lotes calcula el promedio móvil (running mean) y la varianza móvil (running variance) durante el proceso de entrenamiento.

• Cálculo del promedio móvil:

  \(\text{running\_mean} = (1 - \text{momentum}) \times \text{running\_mean} + \text{momentum} \times \mu_B\)

• Cálculo de la varianza móvil:

  \(\text{running\_var} = (1 - \text{momentum}) \times \text{running\_var} + \text{momentum} \times \sigma_B^2\)

Aquí, momentum es un hiperparámetro que generalmente se establece en valores pequeños como 0.1 o 0.01.

Durante la inferencia, se utilizan los running_mean y running_var calculados durante el entrenamiento para normalizar las entradas.

Comparación de la normalización por lotes con otras técnicas de normalización (Normalización por capa, Normalización por instancia, Normalización por grupo)

• Normalización por lotes (Batch Normalization, BN): utiliza las estadísticas entre las muestras dentro de un lote. Se ve afectada por el tamaño del lote y es difícil aplicarla a RNN.

• Normalización por capa (Layer Normalization, LN): usa las estadísticas sobre la dimensión de características para cada muestra. No se ve afectada por el tamaño del lote y es fácil aplicarla a RNN.

• Normalización por instancia (Instance Normalization, IN): calcula las estadísticas independientemente para cada muestra y cada canal. Se utiliza principalmente en tareas de generación de imágenes como la transferencia de estilo (style transfer).

• Normalización por grupo (Group Normalization, GN): divide los canales en grupos y calcula las estadísticas dentro de cada grupo. Puede usarse como una alternativa a BN cuando el tamaño del lote es pequeño.

Cada técnica de normalización tiene sus propias ventajas y desventajas dependiendo de la situación, por lo que se debe elegir la técnica adecuada según las características del problema y la arquitectura del modelo.

6.4.3 Aplicación en el seguimiento estadístico y la inferencia

6.5 Optimización de hiperparámetros

La optimización de hiperparámetros tiene un impacto muy importante en el rendimiento del modelo. Su importancia comenzó a ser conocida desde la década de 1990. A finales de los años 90, se descubrió que en las máquinas de vectores de soporte (SVM), incluso para modelos idénticos, los parámetros de la función kernel (C, gamma, etc.) desempeñaban un papel decisivo en el rendimiento. Alrededor del 2015, se demostró que la optimización bayesiana producía resultados mejores que el ajuste manual, lo que se convirtió en una base fundamental para los métodos de ajuste automatizado (automated tuning) como Google AutoML (2017).

6.5.1 Comparación de metodologías de optimización

Existen varios métodos para optimizar hiperparámetros. Los más representativos son:

1. Búsqueda en cuadrícula (Grid Search): Es el método más básico, donde se especifican listas de valores posibles para cada hiperparámetro y se intentan todas las combinaciones de estos valores. Es útil cuando el número de hiperparámetros es pequeño y el rango de valores que puede tomar cada parámetro está limitado, pero debido a que se deben probar todas las combinaciones, el costo computacional es muy alto. Es adecuado para modelos simples o cuando el espacio de exploración es muy pequeño.

2. Búsqueda aleatoria (Random Search): Se generan combinaciones seleccionando valores aleatorios para cada hiperparámetro y se evalúa el rendimiento del modelo entrenado con estas combinaciones. Si algunos hiperparámetros tienen un impacto significativo en el rendimiento, puede ser más efectivo que la búsqueda en cuadrícula. (Bergstra & Bengio, 2012)

3. Optimización bayesiana (Bayesian Optimization): Selecciona inteligentemente las siguientes combinaciones de hiperparámetros para probar basándose en resultados previos y utilizando un modelo probabilístico (generalmente un proceso gaussiano). Elige el punto que maximiza la función de adquisición (acquisition function) como el siguiente punto a explorar. Dado que explora eficientemente el espacio de búsqueda de hiperparámetros, puede encontrar mejores combinaciones con menos intentos en comparación con la búsqueda en cuadrícula o la búsqueda aleatoria.

Además, existen otros métodos como los algoritmos evolutivos (Evolutionary Algorithms) basados en algoritmos genéticos y la optimización basada en gradientes (Gradient-based Optimization).

A continuación se presenta un ejemplo de cómo optimizar los hiperparámetros de un modelo de red neuronal simple utilizando optimización bayesiana.

6.5.2 Optimización con Bayes-Opt

La optimización bayesiana comenzó a recibir atención desde la década de 2010. En particular, tras la publicación del artículo “Practical Bayesian Optimization of Machine Learning Algorithms” en 2015, ganó una ventaja significativa al seleccionar inteligentemente los siguientes parámetros a explorar basándose en resultados previos.

La optimización bayesiana se repite principalmente en tres etapas:

1. Muestreo inicial (Initialization): Se seleccionan combinaciones de hiperparámetros aleatoriamente y se entrena el modelo para evaluar su rendimiento, un número de veces especificado por init_points.
2. Construcción del modelo sustituto (Surrogate Model): Se construye un modelo sustituto (generalmente un proceso gaussiano) que modela la relación entre los hiperparámetros y el rendimiento basándose en los resultados experimentales hasta ahora.
3. Optimización de la función de adquisición (Acquisition Function): Se selecciona la combinación de hiperparámetros más prometedora para probar a continuación, utilizando la función de adquisición, que se basa en la información actual (el modelo sustituto) para equilibrar entre “exploración” y “explotación”.
4. Se repiten las etapas 2-3.

import torch
import torch.nn as nn
import torch.optim as optim
from dldna.chapter_04.models.base import SimpleNetwork  
from dldna.chapter_04.utils.data import get_data_loaders, get_device  
from bayes_opt import BayesianOptimization
from dldna.chapter_04.experiments.model_training import train_model, eval_loop  


def train_simple_net(hidden_layers, learning_rate, batch_size, epochs):
    """Trains a SimpleNetwork model with given hyperparameters.
       Uses CIFAR100 dataset and train_model from Chapter 4.
    """
    device = get_device()  # Use the utility function to get device

    # Get data loaders for CIFAR100
    train_loader, test_loader = get_data_loaders(dataset="CIFAR100", batch_size=batch_size)

    # Instantiate the model with specified activation and hidden layers.
    # CIFAR100 images are 3x32x32, so the input size is 3*32*32 = 3072.
    model = SimpleNetwork(act_func=nn.ReLU(), input_shape=3*32*32, hidden_shape=hidden_layers, num_labels=100).to(device)

    # Optimizer: Use Adam
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)

    # Train the model using the training function from Chapter 4
    results = train_model(model, train_loader, test_loader, device, optimizer=optimizer, epochs=epochs, save_dir="./tmp/tune",
                         retrain=True) # retrain=True로 설정

    # Return the final test accuracy
    return results['test_accuracies'][-1]


def train_wrapper(learning_rate, batch_size, hidden1, hidden2):
    """Wrapper function for Bayesian optimization."""
    return train_simple_net(
        hidden_layers=[int(hidden1), int(hidden2)],
        learning_rate=learning_rate,
        batch_size=int(batch_size),
        epochs=10
    )

def optimize_hyperparameters():
    """Runs hyperparameter optimization."""
    # Set the parameter ranges to be optimized.
    pbounds = {
        "learning_rate": (1e-4, 1e-2),
        "batch_size": (64, 256),
        "hidden1": (64, 512),  # First hidden layer
        "hidden2": (32, 256)   # Second hidden layer
    }

    # Create a Bayesian optimization object.
    optimizer = BayesianOptimization(
        f=train_wrapper,
        pbounds=pbounds,
        random_state=1,
        allow_duplicate_points=True
    )

    # Run optimization
    optimizer.maximize(
        init_points=4,
        n_iter=10,
    )

    # Print the best parameters and accuracy
    print("\nBest parameters found:")
    print(f"Learning Rate: {optimizer.max['params']['learning_rate']:.6f}")
    print(f"Batch Size: {int(optimizer.max['params']['batch_size'])}")
    print(f"Hidden Layer 1: {int(optimizer.max['params']['hidden1'])}")
    print(f"Hidden Layer 2: {int(optimizer.max['params']['hidden2'])}")
    print(f"\nBest accuracy: {optimizer.max['target']:.4f}")

if __name__ == "__main__":
    print("Starting hyperparameter optimization...")
    optimize_hyperparameters()

El siguiente ejemplo utiliza el paquete BayesOpt para realizar la optimización de hiperparámetros. El objetivo es entrenar SimpleNetwork (definido en el Capítulo 4) utilizando el conjunto de datos CIFAR100. La función train_wrapper actúa como la función objetivo (objective function) que BayesOpt utilizará, entrenando el modelo con una combinación dada de hiperparámetros y devolviendo la precisión final del test.

pbounds especifica el rango de búsqueda para cada hiperparámetro. En optimizer.maximize, init_points es el número de búsquedas aleatorias iniciales, y n_iter es el número de iteraciones de optimización bayesiana. Por lo tanto, el número total de experimentos es init_points + n_iter.

Al explorar hiperparámetros, hay varios puntos a considerar:

1. Rango de parámetros: Un rango demasiado amplio puede aumentar el tiempo de búsqueda, mientras que un rango demasiado estrecho puede hacer que se pierda el óptimo. Generalmente, la tasa de aprendizaje se establece en una escala logarítmica (1e-4 ~ 1e-2), y el número de neuronas se configura en múltiplos de potencias de 2.
2. Número de iteraciones: El número total de intentos generalmente se establece en aproximadamente (número de parámetros) x 20, lo cual ha demostrado dar buenos resultados empíricamente. En el ejemplo anterior, con 4 parámetros, un total de 14 intentos (init_points=4, n_iter=10) puede ser algo bajo. Para obtener mejores resultados, se puede considerar aumentar n_iter.

6.5.3 Optimización con BoTorch

Recientemente, el framework BoTorch ha ganado atención en el campo de la optimización de hiperparámetros de deep learning. BoTorch es un framework de optimización bayesiana basado en PyTorch desarrollado por FAIR (Facebook AI Research, ahora Meta AI) en 2019. Bayes-Opt es una biblioteca de optimización bayesiana más antigua, que ha estado en desarrollo desde 2016 y se utiliza ampliamente debido a su interfaz intuitiva y simple (API estilo scikit-learn).

Las ventajas y desventajas de las dos bibliotecas son claras.

• BoTorch:
  • Ventajas: Integración con modelos de deep learning, aceleración GPU, alta eficiencia de muestreo, diversas técnicas avanzadas de optimización bayesiana (multi-fidelity, multi-task, optimización bajo restricciones, etc.), soporte para diferenciación automática y otras funcionalidades especializadas en la optimización de hiperparámetros de modelos de deep learning. Es particularmente adecuado para modelos a gran escala, espacios de parámetros de alta dimensión y experimentos con altos costos computacionales.
  • Desventajas: Requiere más aprendizaje en comparación con Bayes-Opt y la configuración inicial puede ser compleja.
• Bayes-Opt:
  • Ventajas: Proporciona una API simple e intuitiva que facilita su uso. La instalación es sencilla y cuenta con abundantes tutoriales y ejemplos de código.
  • Desventajas: En comparación con BoTorch, carece de funciones avanzadas y la integración con modelos de deep learning es menos fluida. El rendimiento puede disminuir en problemas a gran escala o de alta dimensión.

Por lo tanto, para problemas simples o la creación rápida de prototipos, se recomienda Bayes-Opt; mientras que para la optimización compleja de hiperparámetros de modelos de deep learning, problemas a gran escala o de alta dimensión y técnicas avanzadas de optimización bayesiana (por ejemplo, multi-task, optimización con restricciones), es preferible usar BoTorch.

Para utilizar BoTorch, a diferencia de Bayes-Opt, es necesario comprender algunos conceptos clave necesarios para la configuración inicial (modelos surrogados, normalización de datos de entrada, funciones de adquisición).

1. Modelo Surrogate:

   El modelo surrogate es un modelo que aproxima la función objetivo real (en este caso, la precisión de validación del modelo de deep learning). Generalmente se utiliza el proceso gaussiano (GP). El GP se usa para predecir resultados rápidamente y a bajo costo en lugar de la costosa función objetivo real. BoTorch ofrece los siguientes modelos GP:

   • SingleTaskGP: Es el modelo de proceso gaussiano más básico. Es adecuado para problemas de optimización de un solo objetivo (single-objective) y es efectivo con conjuntos de datos relativamente pequeños, de 1000 puntos o menos.
   • MultiTaskGP: Se usa cuando se necesita optimizar varias funciones objetivas simultáneamente (optimización multi-objetivo). Por ejemplo, puede optimizar tanto la precisión del modelo como el tiempo de inferencia.
   • SAASBO (Sparsity-Aware Adaptive Subspace Bayesian Optimization): Es un modelo especializado para espacios de parámetros de alta dimensión. Asume que existe una dispersión en los espacios de alta dimensión y realiza búsquedas eficientes.

2. Normalización de datos de entrada:

   El proceso gaussiano es sensible a la escala de los datos, por lo que es importante normalizar los datos de entrada (hiperparámetros). Generalmente, todos los hiperparámetros se transforman al rango [0, 1]. BoTorch proporciona las transformaciones Normalize y Standardize.

3. Función de Adquisición (Acquisition Function): La función de adquisición se basa en un modelo proxy (GP) para determinar la próxima combinación de hiperparámetros a probar. La función de adquisición juega el papel de equilibrar entre “exploración” y “explotación”. BoTorch proporciona las siguientes funciones de adquisición.

• ExpectedImprovement (EI): Es una de las funciones de adquisición más comunes. Considera la probabilidad de obtener un resultado mejor que el óptimo actual y el grado de mejora.
• LogExpectedImprovement (LogEI): Es una versión logarítmica transformada del EI. Es numéricamente más estable y responde con mayor sensibilidad a pequeños cambios.
• UpperConfidenceBound (UCB): Una función de adquisición que pone más énfasis en la exploración. Explora activamente las regiones de alta incertidumbre.
• ProbabilityOfImprovement (PI): Indica la probabilidad de mejorar el valor óptimo actual.
• qExpectedImprovement (qEI): También conocido como q-batch EI, se utiliza para optimización paralela. Selecciona múltiples candidatos a la vez.
• qNoisyExpectedImprovement (qNEI): q-batch Noisy EI. Se usa en entornos ruidosos.

El código completo está en package/botorch_optimization.py. Puede ejecutarse directamente desde la línea de comandos. El código completo incluye comentarios detallados, por lo que aquí solo se explicarán las partes importantes de cada código.

def __init__(self, max_trials: int = 80, init_samples: int = 10):
    self.param_bounds = torch.tensor([
        [1e-4, 64.0, 32.0, 32.0],      # 최소값
        [1e-2, 256.0, 512.0, 512.0]    # 최대값
    ], dtype=torch.float64)

En la parte de inicialización, se establecen los valores mínimos y máximos de cada hiperparámetro. max_trials es el número total de intentos, e init_samples es el número de experimentos aleatorios iniciales (equivalente a init_points en Bayes-Opt). init_samples generalmente se configura como 2 o 3 veces el número de parámetros. En el ejemplo anterior, hay 4 hiperparámetros, por lo que un valor adecuado sería entre 8 y 12. Se utiliza torch.float64 para asegurar la estabilidad numérica. La optimización bayesiana, especialmente los procesos gaussianos, utilizan descomposición de Cholesky en el cálculo de matrices de kernel, y durante este proceso, float32 puede generar errores debido a problemas de precisión.

def tune(self):
    # 가우시안 프로세스 모델 학습
    model = SingleTaskGP(configs, accuracies)
    mll = ExactMarginalLogLikelihood(model.likelihood, model)
    fit_gpytorch_mll(mll)

Se utiliza un modelo proxy basado en procesos gaussianos llamado SingleTaskGP. ExactMarginalLogLikelihood es la función de pérdida utilizada para el entrenamiento del modelo, y fit_gpytorch_mll entrena el modelo utilizando esta función de pérdida.

acq_func = LogExpectedImprovement(
    model, 
    best_f=accuracies.max().item()
)

Se utiliza la función de adquisición LogExpectedImprovement. Debido al uso del logaritmo, es numéricamente estable y responde sensiblemente a pequeños cambios.

candidate, _ = optimize_acqf(                                   # 획득 함수 최적화로 다음 실험할 파라미터 선택
    acq_func, bounds=bounds,                                    # 획득 함수와 파라미터 범위 지정
    q=1,                                                        # 한 번에 하나의 설정만 선택
    num_restarts=10,                                            # 최적화 재시작 횟수
    raw_samples=512                                             # 초기 샘플링 수
)

optimize_acqf es una función que optimiza la función de adquisición para seleccionar la combinación de hiperparámetros (candidate) a experimentar a continuación.

• q=1: solo selecciona un candidato a la vez (no es una optimización en q-batch).
• num_restarts=10: durante cada paso de optimización, se repite 10 veces desde diferentes puntos de inicio para evitar caer en mínimos locales.
• raw_samples=512: se extraen 512 muestras del proceso gaussiano para estimar el valor de la función de adquisición.

num_restarts y raw_samples tienen un impacto significativo en el equilibrio entre exploración y explotación en la optimización bayesiana. num_restarts determina la exhaustividad de la optimización, mientras que raw_samples afecta a la precisión de la estimación de la función de adquisición. Cuanto mayores sean estos valores, mayor será el costo computacional, pero también aumentará la probabilidad de obtener mejores resultados. En general, se pueden usar los siguientes valores:

• Ejecución rápida: num_restarts=5, raw_samples=256
• Equilibrio: num_restarts=10, raw_samples=512
• Foco en precisión: num_restarts=20, raw_samples=1024

from dldna.chapter_06.botorch_optimizer import run_botorch_optimization

run_botorch_optimization(max_trials=80, init_samples=5)

Resultado Dataset : FashionMNIST Épocas : 20 Experimentos iniciales : 5 veces Experimentos de repetición : 80 veces

Parámetro óptimo	Bayes-Opt	Botorch
Tasa de aprendizaje	6e-4	1e-4
Tamaño del lote	173	158
hid 1	426	512
hid 2	197	512
Precisión	0.7837	0.8057

Es una comparación simple, pero la precisión de BoTorch es mayor. Para búsquedas de optimización simples se recomienda Bayes-Opt y para exploraciones especializadas se recomienda BoTorch.

6.6 Procesos Gaussianos

Desafío: ¿Cuál es el método para cuantificar la incertidumbre de las predicciones del modelo y utilizarla para aprender activamente?

Reflexión del investigador: Los modelos de aprendizaje profundo tradicionales proporcionan estimaciones puntuales (point estimates) como resultados de predicción, pero en aplicaciones reales es muy importante conocer la incertidumbre de las predicciones. Por ejemplo, un automóvil autónomo debe saber qué tan incierta es su predicción sobre el próximo movimiento de un peatón para poder conducir de manera segura. Los procesos Gaussianos han sido una herramienta poderosa basada en la teoría Bayesiana para cuantificar la incertidumbre de las predicciones, pero tienen la desventaja de ser computacionalmente complejos y difíciles de aplicar a conjuntos de datos grandes.

Los Procesos Gaussianos (Gaussian Process, GP) son modelos clave en el aprendizaje Bayesiano que proporcionan predicciones con conciencia de incertidumbre. Anteriormente, vimos brevemente cómo los procesos Gaussianos se utilizan como modelo sustituto (surrogate model) en la optimización Bayesiana; aquí, exploraremos más detalladamente los principios fundamentales y la importancia de los procesos Gaussianos.

Un GP se define como una “distribución de probabilidad sobre un conjunto de valores de función”. A diferencia de una función determinista \(y = f(x)\) que predice un solo valor de salida para una entrada dada, un GP no predice un solo valor de salida \(y\) para una entrada dada \(x\), sino una distribución de posibles valores de salida. Por ejemplo, en lugar de predecir con certeza “la temperatura máxima mañana será 25 grados”, podría predecir “hay una probabilidad del 95% de que la temperatura máxima mañana esté entre 23 y 27 grados”. Si estás conduciendo en bicicleta hacia casa, el camino general ya está decidido, pero cada vez puede variar. Se necesita un tipo de predicción que incluya incertidumbre, no una predicción determinista.

La base matemática para manejar predicciones con incertidumbre se encuentra en la distribución normal (distribución Gaussiana) propuesta por el matemático del siglo XIX, Gauss. Sobre esta base, los procesos Gaussianos se desarrollaron en la década de 1940. En ese momento, durante la Segunda Guerra Mundial, los científicos tenían que manejar datos inciertos como nunca antes, incluyendo el procesamiento de señales de radar, descifrado de códigos y análisis meteorológico. Un ejemplo notable es el trabajo de Norbert Wiener para mejorar la precisión del cañón antiaéreo al predecir la futura posición de los aviones. Wiener concibió un “proceso Wiener” que veía el movimiento de los aviones como un proceso estocástico, donde la incertidumbre era fundamental. En 1951, Daniel Krige aplicó los procesos Gaussianos para predecir la distribución de vetas minerales. Hasta los años 70, los estadísticos sistematizaron las aplicaciones de los procesos Gaussianos en estadística espacial, diseño de experimentos computacionales y optimización Bayesiana en el aprendizaje automático. Hoy en día, desempeñan un papel crucial en casi todos los campos que manejan incertidumbre, incluyendo la inteligencia artificial, robótica y predicción climática. En particular, en el aprendizaje profundo, los procesos Gaussianos con kernels profundos a través del aprendizaje meta (meta-learning) han recibido atención reciente y muestran un rendimiento destacado en campos como la predicción de características moleculares.

Hoy en día, los procesos Gaussianos se utilizan en una amplia gama de campos, incluyendo inteligencia artificial, robótica y modelización climática. En particular, en el aprendizaje profundo, recientemente han destacado los procesos Gaussianos con kernels profundos a través del aprendizaje meta (meta-learning) y la predicción de características moleculares.

Haga clic para ver el contenido (profundización: fundamentos matemáticos de los procesos gaussianos y sus aplicaciones en machine learning)

Fundamentos matemáticos del proceso gaussiano y aplicaciones en el aprendizaje automático

El proceso gaussiano (Gaussian Process, GP) es un modelo probabilístico basado en métodos de núcleo (kernel method), que se utiliza ampliamente para problemas de regresión y clasificación. El GP tiene la ventaja de definir una distribución sobre las funciones mismas, lo que permite cuantificar la incertidumbre en las predicciones. En este profundización detallada, exploramos los fundamentos matemáticos del proceso gaussiano desde la distribución normal multivariante (multivariate normal distribution) hasta la perspectiva de procesos estocásticos (stochastic process), y examinamos diversas aplicaciones en el aprendizaje automático.

1. Distribución normal multivariante (Multivariate Normal Distribution)

El primer paso para entender los procesos gaussianos es comprender la distribución normal multivariante. Un vector aleatorio \(\mathbf{x} = (x_1, x_2, ..., x_d)^T\) de dimensión \(d\) que sigue una distribución normal multivariante significa que tiene la siguiente función de densidad de probabilidad (probability density function).

\(p(\mathbf{x}) = \frac{1}{(2\pi)^{d/2}|\mathbf{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)\)

Donde \(\boldsymbol{\mu} \in \mathbb{R}^d\) es el vector de medias, y \(\mathbf{\Sigma} \in \mathbb{R}^{d \times d}\) es la matriz de covarianza (covariance matrix). La matriz de covarianza debe ser una matriz definida positiva (positive definite).

Propiedades clave:

• Transformación lineal: La transformación lineal de una variable aleatoria que sigue una distribución normal multivariante también seguirá una distribución normal multivariante. Es decir, si \(\mathbf{x} \sim \mathcal{N}(\boldsymbol{\mu}, \mathbf{\Sigma})\) y \(\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{b}\), entonces \(\mathbf{y} \sim \mathcal{N}(\mathbf{A}\boldsymbol{\mu} + \mathbf{b}, \mathbf{A}\mathbf{\Sigma}\mathbf{A}^T)\).

• Distribución condicional (Conditional Distribution): La distribución condicional de una distribución normal multivariante también sigue una distribución normal. Si dividimos \(\mathbf{x}\) en \(\mathbf{x} = (\mathbf{x}_1, \mathbf{x}_2)^T\) y las medias y matrices de covarianza se dividen como:

  \(\boldsymbol{\mu} = \begin{pmatrix} \boldsymbol{\mu}_1 \\ \boldsymbol{\mu}_2 \end{pmatrix}, \quad \mathbf{\Sigma} = \begin{pmatrix} \mathbf{\Sigma}_{11} & \mathbf{\Sigma}_{12} \\ \mathbf{\Sigma}_{21} & \mathbf{\Sigma}_{22} \end{pmatrix}\)

  La distribución condicional de \(\mathbf{x}_2\) dado \(\mathbf{x}_1\) es:

  \(p(\mathbf{x}_2 | \mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu}_{2|1}, \mathbf{\Sigma}_{2|1})\)

  \(\boldsymbol{\mu}_{2|1} = \boldsymbol{\mu}_2 + \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}(\mathbf{x}_1 - \boldsymbol{\mu}_1)\) \(\mathbf{\Sigma}_{2|1} = \mathbf{\Sigma}_{22} - \mathbf{\Sigma}_{21}\mathbf{\Sigma}_{11}^{-1}\mathbf{\Sigma}_{12}\)

• Distribución marginal (Marginal Distribution): La distribución marginal de una distribución normal multivariante también sigue una distribución normal. Dado el particionamiento anterior, la distribución marginal de \(\mathbf{x}_1\) es la siguiente. \(p(\mathbf{x}_1) = \mathcal{N}(\boldsymbol{\mu_1}, \mathbf{\Sigma}_{11})\)

2. Definición del proceso gaussiano y su interpretación desde una perspectiva de procesos estocásticos

El proceso gaussiano es una distribución de probabilidad sobre funciones. Es decir, que una función \(f(x)\) siga un proceso gaussiano significa que el vector de valores de la función \((f(x_1), f(x_2), ..., f(x_n))^T\) para cualquier conjunto finito de puntos de entrada \(\{x_1, x_2, ..., x_n\}\) sigue una distribución normal multivariante.

Definición: Un proceso gaussiano se define por la función media (mean function) \(m(x)\) y la función de covarianza (o kernel function) \(k(x, x')\).

\(f(x) \sim \mathcal{GP}(m(x), k(x, x'))\)

• Función media: \(m(x) = \mathbb{E}[f(x)]\)
• Función de covarianza: \(k(x, x') = \mathbb{E}[(f(x) - m(x))(f(x') - m(x'))]\)

Perspectiva del proceso estocástico (Stochastic Process): Un proceso gaussiano es un tipo de proceso estocástico que asigna una variable aleatoria al conjunto índice (aquí, el espacio de entrada). En un proceso gaussiano, estas variables aleatorias siguen una distribución normal conjunta.

3. El papel de la función kernel y introducción a diferentes funciones kernel

La función kernel es uno de los elementos más importantes en un proceso gaussiano. La función kernel representa la similitud entre dos entradas \(x\) y \(x'\), y determina las propiedades del proceso gaussiano.

Roles clave:

• Definición de covarianza: La función kernel define la covarianza entre los valores de la función. Es decir, \(k(x, x')\) representa la covarianza entre \(f(x)\) y \(f(x')\).
• Determinación de suavidad (Smoothness): La función kernel determina la suavidad de las funciones generadas. Por ejemplo, el kernel RBF genera funciones infinitamente diferenciables, mientras que el kernel Matern permite controlar la diferenciabilidad.
• Positividad definida (Positive Definiteness): Para ser una función de covarianza válida, la función kernel debe cumplir con la positividad definida. Es decir, la matriz kernel generada a partir de cualquier conjunto de puntos de entrada debe ser una matriz positiva definida.

Diferentes funciones kernel:

• Kernel RBF (Radial Basis Function) (o kernel Exponencial Cuadrático):

  \(k(x, x') = \sigma^2 \exp\left(-\frac{\|x - x'\|^2}{2l^2}\right)\)

  • \(\sigma^2\): varianza
  • \(l\): escala de longitud (length scale)
  • Genera funciones muy suaves.

• Kernel Matern:

  \(k(x, x') = \sigma^2 \frac{2^{1-\nu}}{\Gamma(\nu)}\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)^\nu K_\nu\left(\sqrt{2\nu}\frac{\|x - x'\|}{l}\right)\)

• \(\nu\): parámetro de suavidad (smoothness parameter)

• \(K_\nu\): función de Bessel modificada (modified Bessel function)

• Se utilizan principalmente valores semienteros (half-integer) como \(\nu = 1/2, 3/2, 5/2\).

• A medida que \(\nu\) aumenta, se acerca al núcleo RBF.

• Núcleo periódico (Periodic):

  \(k(x, x') = \sigma^2 \exp\left(-\frac{2\sin^2(\pi|x-x'|/p)}{l^2}\right)\)

  • \(p\) : período

• Núcleo lineal (Linear):

  \(k(x,x') = \sigma_b^2 + \sigma_v^2(x - c)(x' -c)\)

4. Resolución de problemas de regresión y clasificación utilizando procesos gaussianos

Regresión:

La regresión con procesos gaussianos consiste en predecir la salida \(f(\mathbf{x}_*)\) para una nueva entrada \(\mathbf{x}_*\) basada en los datos de entrenamiento \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n\). Se combina la distribución previa (prior distribution) del proceso gaussiano con los datos de entrenamiento para calcular la distribución posterior (posterior distribution), a partir de la cual se obtiene la distribución predictiva (predictive distribution).

• Distribución previa: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\) (se asume una función media de 0 por conveniencia)
• Datos de entrenamiento: \(\mathbf{y} = (y_1, y_2, ..., y_n)^T\)
• Matriz del núcleo: \(\mathbf{K} = k(\mathbf{X}, \mathbf{X})\), donde \(\mathbf{X} = [\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_n]\)
• Distribución predictiva: \(p(f(\mathbf{x}_*) | \mathbf{y}, \mathbf{X}, \mathbf{x}_*) = \mathcal{N}(\mu_*, \sigma_*^2)\)
  • \(\mu_* = \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{y}\)
  • \(\sigma_*^2 = k(\mathbf{x}_*, \mathbf{x}_*) - \mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{k}_*\)
  • \(\mathbf{k}_* = [k(\mathbf{x}_*, \mathbf{x}_1), k(\mathbf{x}_*, \mathbf{x}_2), ..., k(\mathbf{x}_*, \mathbf{x}_n)]^T\)

Clasificación:

La clasificación con procesos gaussianos implica modelar la función latente (latent function) \(f(\mathbf{x})\) como un proceso gaussiano y definir las probabilidades de clasificación a través de esta función latente. Por ejemplo, en problemas de clasificación binaria, se utilizan funciones logísticas o probit para convertir los valores de la función latente en probabilidades.

• Función latente: \(f(\mathbf{x}) \sim \mathcal{GP}(0, k(\mathbf{x}, \mathbf{x}'))\)
• Clasificación binaria: \(p(y = 1 | f(\mathbf{x})) = \sigma(f(\mathbf{x}))\) (donde \(\sigma\) es la función logística)

En problemas de clasificación, como la distribución posterior no tiene una forma cerrada, se utilizan métodos de inferencia aproximada como la aproximación de Laplace o la inferencia variacional. ### 5. Ventajas y desventajas del proceso gaussiano y comparación con el aprendizaje profundo

Ventajas:

• Cuantificación de la incertidumbre: proporciona la incertidumbre de las predicciones en forma de varianza predictiva.
• Eficiencia de datos: puede ofrecer un buen rendimiento con una cantidad relativamente pequeña de datos.
• Flexibilidad en la selección del kernel: se pueden usar diversas funciones de kernel para diseñar un modelo adecuado a las características del problema.
• Interpretación bayesiana: se interpreta naturalmente dentro del marco bayesiano.

Desventajas:

• Complejidad computacional: tiene una complejidad computacional de \(O(n^3)\) en función del tamaño \(n\) de los datos de entrenamiento. (debido al cálculo de la matriz inversa)
• Selección del modelo: es importante y puede ser difícil elegir la función de kernel y los hiperparámetros adecuados.
• Entradas de alta dimensión: el rendimiento puede disminuir en espacios de entrada de alta dimensión.

Comparación con el aprendizaje profundo:

• Requisitos de datos: los modelos de aprendizaje profundo generalmente requieren una cantidad mucho mayor de datos que el proceso gaussiano.
• Costo computacional: los modelos de aprendizaje profundo requieren un alto costo computacional para el entrenamiento, pero la inferencia es relativamente rápida. El proceso gaussiano puede ser rápido en el entrenamiento (cuando hay pocos datos), pero la inferencia tiene un costo computacional que aumenta con el tamaño de los datos.
• Incertidumbre: generalmente, los modelos de aprendizaje profundo no proporcionan incertidumbre en las predicciones. (aunque existen excepciones como el aprendizaje profundo bayesiano).
• Expresividad: los modelos de aprendizaje profundo pueden representar funciones muy complejas, mientras que la expresividad del proceso gaussiano está limitada por la función de kernel.
• Interpretabilidad: el proceso gaussiano puede explicitar las suposiciones del modelo a través de la función de kernel y proporciona una cuantificación de la incertidumbre en los resultados de predicción.

Recientemente, se están investigando modelos que combinan el aprendizaje profundo y el proceso gaussiano (por ejemplo, Deep Kernel Learning).

6.6.1 Fundamentos matemáticos para el manejo de la incertidumbre

Generalmente pensamos en una función como una sola línea, pero los procesos gaussianos la consideran un “conjunto de varias líneas posibles”. Matemáticamente, esto se expresa de la siguiente manera:

\(f(t) \sim \mathcal{GP}(m(t), k(t,t'))\)

Tomando el ejemplo de la posición de una bicicleta, \(m(t)\) es la función media que indica “probablemente seguirá esta ruta”. \(k(t,t')\) es la función de covarianza (o kernel) que muestra “hasta qué punto las posiciones en diferentes momentos están relacionadas”. Hay varios kernels típicos. Uno de los kernels más utilizados es el RBF (Función Base Radial).

\(k(t,t') = \sigma^2 \exp\left(-\frac{(t-t')^2}{2l^2}\right)\)

Esta fórmula es muy intuitiva. Cuanto más cerca estén dos momentos \(t\) y \(t'\), mayor será el valor; cuanto más lejos estén, menor será el valor. Es como si “si sabemos nuestra posición actual, podemos predecir bastante bien la posición en un corto tiempo después, pero no tanto para un futuro lejano”.

Si consideramos que \(K\) es RBF y vemos un ejemplo práctico. Imagina que tienes un servicio de bicicletas compartidas (o vehículos autónomos también serviría). Queremos estimar la ruta completa de una bicicleta basándonos solo en algunas observaciones GPS.

Fórmula básica para la predicción

\(f_* | X, y, X_* \sim \mathcal{N}(\mu_*, \Sigma_*)\)

Esta fórmula expresa que “basándonos en nuestros registros GPS (\(X\), \(y\)), la posición de la bicicleta en los momentos desconocidos (\(X_*\)) sigue una distribución normal con media \(\mu_*\) y varianza \(\Sigma_*\)”.

Cálculo de la predicción de la posición

\(\mu_* = K_*K^{-1}y\)

Esta fórmula muestra cómo predecir la posición de la bicicleta. \(K_*\) representa la “correlación temporal” entre los momentos a predecir y los momentos registrados por GPS; \(K^{-1}\) ajusta el “peso” considerando las relaciones entre los registros de GPS, y \(y\) son las posiciones reales registradas por GPS. Por ejemplo, para predecir la posición a las 2:15 p.m.: 1. Consideramos los registros GPS a las 2:00 p.m. y 2:30 p.m. 2. Y ajustamos el peso basándonos en la consistencia de esos registros.

Efecto de la incertidumbre según los datos La incertidumbre en la predicción varía según la cantidad de datos GPS: 1. En intervalos con muchos registros GPS: baja incertidumbre - \(K_*\) es grande y hay muchos datos, por lo que \(K_*K^{-1}K_*^T\) también es grande - Por tanto, \(\Sigma_*\) es pequeño y la estimación de la ruta es precisa. 2. En intervalos con pocos registros GPS: alta incertidumbre - \(K_*\) es pequeño y hay pocos datos, por lo que \(K_*K^{-1}K_*^T\) también es pequeño - Por tanto, \(\Sigma_*\) es grande y la incertidumbre en la estimación de la ruta es alta.

En resumen, cuanto más densos sean los datos en intervalos de tiempo, mayor será el valor de \(K\), lo que reduce la incertidumbre.

Veamos un ejemplo para entender mejor cómo se predice la ruta de una bicicleta.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 시각화 스타일 설정
sns.set_style("whitegrid")
plt.rcParams['font.size'] = 10

# 데이터셋 1: 5개 관측점
time1 = np.array([0, 2, 5, 8, 10]).reshape(-1, 1)
position1 = np.array([0, 2, 3, 1, 4])

# 데이터셋 2: 8개 관측점
time2 = np.array([0, 1, 2, 4, 5, 6, 8, 10]).reshape(-1, 1)
position2 = np.array([0, 1, 2.5, 1.5, 3, 2, 1, 4])  # 더 큰 변동성 추가

# 예측할 시간점 생성: 0~10분 구간을 100개로 분할
time_pred = np.linspace(0, 10, 100).reshape(-1, 1)

# RBF 커널 함수 정의
def kernel(T1, T2, l=2.0):
    sqdist = np.sum(T1**2, 1).reshape(-1, 1) + np.sum(T2**2, 1) - 2 * np.dot(T1, T2.T)
    return np.exp(-0.5 * sqdist / l**2)

# 가우시안 프로세스 예측 함수
def predict_gp(time, position, time_pred):
    K = kernel(time, time)
    K_star = kernel(time_pred, time)
    K_star_star = kernel(time_pred, time_pred)
    mu_star = K_star.dot(np.linalg.inv(K)).dot(position)
    sigma_star = K_star_star - K_star.dot(np.linalg.inv(K)).dot(K_star.T)
    return mu_star, sigma_star

# 두 데이터셋에 대한 예측 수행
mu1, sigma1 = predict_gp(time1, position1, time_pred)
mu2, sigma2 = predict_gp(time2, position2, time_pred)

# 2개의 서브플롯 생성
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 4))

# 첫 번째 그래프 (5개 데이터)
ax1.fill_between(time_pred.flatten(),
                mu1 - 2*np.sqrt(np.diag(sigma1)),
                mu1 + 2*np.sqrt(np.diag(sigma1)),
                color='blue', alpha=0.2, label='95% confidence interval')
ax1.plot(time_pred, mu1, 'b-', linewidth=1.5, label='Predicted path')
ax1.plot(time1, position1, 'ro', markersize=6, label='GPS records')
ax1.set_xlabel('Time (min)')
ax1.set_ylabel('Position (km)')
ax1.set_title('Route Estimation (5 GPS points)')
ax1.legend(fontsize=8)

# 두 번째 그래프 (8개 데이터)
ax2.fill_between(time_pred.flatten(),
                mu2 - 2*np.sqrt(np.diag(sigma2)),
                mu2 + 2*np.sqrt(np.diag(sigma2)),
                color='blue', alpha=0.2, label='95% confidence interval')
ax2.plot(time_pred, mu2, 'b-', linewidth=1.5, label='Predicted path')
ax2.plot(time2, position2, 'ro', markersize=6, label='GPS records')
ax2.set_xlabel('Time (min)')
ax2.set_ylabel('Position (km)')
ax2.set_title('Route Estimation (8 GPS points)')
ax2.legend(fontsize=8)

plt.tight_layout()
plt.show()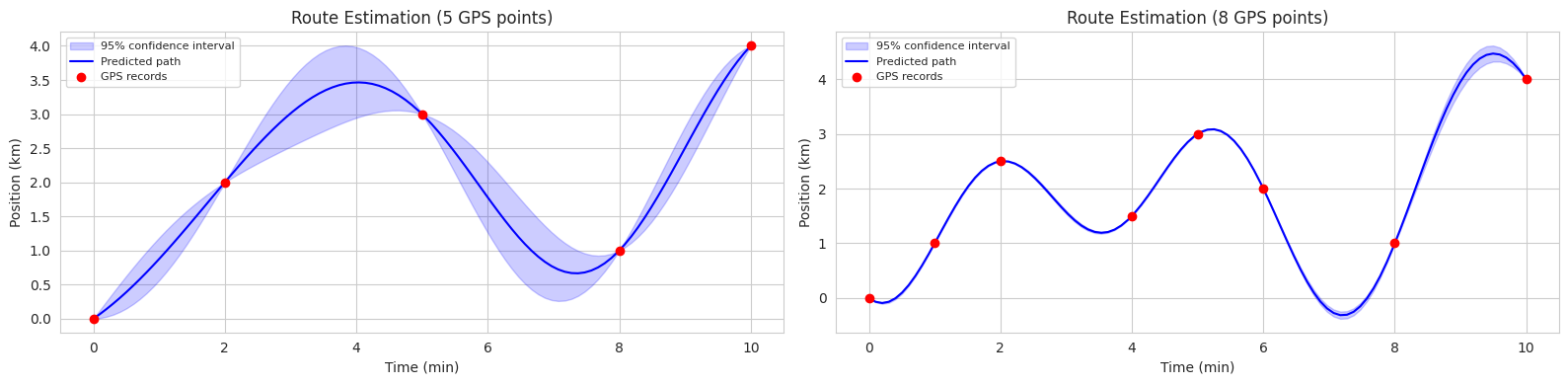

El siguiente código es un ejemplo de la estimación de rutas de bicicleta utilizando procesos gaussianos (GP) en dos escenarios (5 puntos de observación, 8 puntos de observación). En cada gráfico, la línea sólida azul representa la ruta media predicha, y el área sombreada azul muestra el intervalo de confianza del 95%.

• Cuando hay pocos datos (gráfico izquierdo): Debido a que los registros GPS son dispersos, la incertidumbre en las predicciones (el ancho del intervalo de confianza) es alta.
• Cuando hay muchos datos (gráfico derecho): Con registros GPS más densos, la incertidumbre en las predicciones disminuye y la ruta predicha se aproxima más a la ruta real.

De esta manera, los GP no solo proporcionan resultados de predicción, sino también su incertidumbre, lo que los hace útiles en diversos campos donde es necesario considerar la incertidumbre en el proceso de toma de decisiones (por ejemplo: conducción autónoma, control de robots, diagnóstico médico).

6.6.2 Aplicaciones modernas

Los procesos gaussianos se aplican en diversas áreas científicas e ingenierísticas, como el control de robots, la optimización de redes de sensores, la predicción de estructuras moleculares, la modelación climática y el análisis de datos astrofísicos. En el campo del aprendizaje automático (machine learning), una aplicación representativa es la optimización de hiperparámetros, como se ha discutido anteriormente. Otro campo representativo que requiere predicciones con incertidumbre es la conducción autónoma de vehículos. Se predice la futura posición del vehículo relativo y en los intervalos de mayor incertidumbre, se conduce de manera más defensiva. Además, se aplican ampliamente en el campo médico para predecir cambios en el estado del paciente, y en los mercados financieros para predecir precios de acciones y gestionar riesgos basados en la incertidumbre. Recientemente, las aplicaciones de GP están siendo activamente investigadas en campos como el aprendizaje por refuerzo (reinforcement learning), la combinación con modelos generativos en el aprendizaje profundo (deep learning), la inferencia causal y el aprendizaje meta (meta-learning).

6.6.3 Aprendizaje de núcleos profundos (Deep Kernel Learning)

El aspecto más importante de los procesos gaussianos es el kernel (función de covarianza). El aprendizaje profundo tiene una ventaja en aprender representaciones a partir de datos. La combinación eficiente de la capacidad predictiva de GP y la capacidad de aprendizaje de representaciones del aprendizaje profundo es una dirección de investigación natural. Un método representativo es el Aprendizaje de Núcleos Profundos (Deep Kernel Learning, DKL), que utiliza redes neuronales para aprender directamente el kernel a partir de los datos en lugar de predefinir un kernel como el RBF.

La estructura general del DKL es la siguiente:

1. Extracción de características (Feature Extraction): Los datos de entrada pasan primero por una red neuronal profunda (generalmente una CNN o una Transformer) para convertirse en vectores de características de baja dimensión.
2. Cálculo del núcleo (Kernel Computation): Se utiliza la función kernel del proceso gaussiano (por ejemplo, el kernel RBF) con los vectores de características extraídos como entrada para calcular la matriz de kernel.
3. Proceso gaussiano (Gaussian Process): Se entrena un modelo de proceso gaussiano utilizando la matriz de kernel calculada y los datos de entrenamiento, y se realiza una predicción (media y varianza) para nuevas entradas. El DKL tiene la ventaja de poder aprender simultáneamente representaciones útiles a partir de los datos y la similitud entre los datos mediante redes neuronales. Esto permite realizar predicciones que consideran la incertidumbre en datos complejos (por ejemplo, imágenes, gráficos, texto).

El DKL se utiliza en diversos campos. * Clasificación de imágenes (Image Classification): Se utilizan CNN para extraer características de las imágenes y GP para realizar la clasificación. * Clasificación de grafos (Graph Classification): Se usan redes neuronales de grafos (GNN) para extraer características de la estructura del grafo y GP para realizar la clasificación del grafo. * Predicción de propiedades moleculares (Molecular Property Prediction): Acepta gráficos moleculares como entrada y predice las propiedades de la molécula (por ejemplo, solubilidad, toxicidad). * Predicción de series temporales (Time Series Forecasting): Se utilizan RNN para extraer características de los datos de serie temporal y GP para predecir valores futuros. Aquí se ejecutará un simple ejemplo de DKL y en la parte 2 se explorarán más detalles y casos de aplicación.

Redes de núcleos profundas

Primero, definimos las redes de núcleos profundas. Las redes de núcleos son redes neuronales que aprenden funciones de núcleo. Esta red neuronal recibe datos de entrada y produce representaciones de características. Estas representaciones de características se utilizan para calcular la matriz de núcleo.

import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Normal
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# Set seed for reproducibility
torch.manual_seed(42)
np.random.seed(42)

# Define a neural network to learn the kernel
class DeepKernel(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(DeepKernel, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, hidden_dim)
        self.fc3 = nn.Linear(hidden_dim, output_dim)
        self.activation = nn.ReLU()

    def forward(self, x):
        x = self.activation(self.fc1(x))
        x = self.activation(self.fc2(x))
        x = self.fc3(x)  # No activation on the final layer
        return x

La entrada de una red neuronal de kernel profundo es típicamente un tensor 2D, donde la primera dimensión es el tamaño del lote y la segunda dimensión es la dimensión de los datos de entrada. La salida es un tensor 2D de forma (tamaño del lote, dimensión de representación de características).

Definición de la capa GP

La capa GP recibe la salida de la red de kernel profundo, calcula la matriz de kernel y determina la distribución predictiva.

import torch
import torch.nn as nn

# Define the Gaussian Process layer
class GaussianProcessLayer(nn.Module):
    def __init__(self, num_dim, num_data):
        super(GaussianProcessLayer, self).__init__()
        self.num_dim = num_dim
        self.num_data = num_data
        self.lengthscale = nn.Parameter(torch.ones(num_dim))  # Length-scale for each dimension
        self.noise_var = nn.Parameter(torch.ones(1))  # Noise variance
        self.outputscale = nn.Parameter(torch.ones(1))  # Output scale

    def forward(self, x, y):
        # Calculate the kernel matrix (using RBF kernel)
        dist_matrix = torch.cdist(x, x)  # Pairwise distances between inputs
        kernel_matrix = self.outputscale * torch.exp(-0.5 * dist_matrix**2 / self.lengthscale**2)
        kernel_matrix += self.noise_var * torch.eye(self.num_data)

        # Calculate the predictive distribution (using Cholesky decomposition)
        L = torch.linalg.cholesky(kernel_matrix)
        alpha = torch.cholesky_solve(y.unsqueeze(-1), L)  # Add unsqueeze for correct shape
        predictive_mean = torch.matmul(kernel_matrix, alpha).squeeze(-1) # Remove extra dimension
        v = torch.linalg.solve_triangular(L, kernel_matrix, upper=False)
        predictive_var = kernel_matrix - torch.matmul(v.T, v)


        return predictive_mean, predictive_var

        return predictive_mean, predictive_var

La entrada de la capa GP es un tensor 2D de forma (tamaño del lote, dimensión de representación de características). La salida es una tupla que incluye la media y la varianza predichas. Para el cálculo de la matriz kernel se utiliza el kernel RBF, y para calcular la distribución predictiva se aprovecha la descomposición de Cholesky (Cholesky decomposition) para mejorar la eficiencia computacional. y.unsqueeze(-1) y .squeeze(-1) se utilizan para ajustar las dimensiones entre y y la matriz kernel.

# 데이터를 생성
x = np.linspace(-10, 10, 100)
y = np.sin(x) + 0.1 * np.random.randn(100)

# 데이터를 텐서로 변환
x_tensor = torch.tensor(x, dtype=torch.float32).unsqueeze(-1)  # (100,) -> (100, 1)
y_tensor = torch.tensor(y, dtype=torch.float32)  # (100,)


# 딥 커널과 GP 레이어를 초기화
deep_kernel = DeepKernel(input_dim=1, hidden_dim=50, output_dim=1)  # output_dim=1로 수정
gp_layer = GaussianProcessLayer(num_dim=1, num_data=len(x))

# 손실 함수와 최적화기를 정의
loss_fn = nn.MSELoss()  # Use MSE loss
optimizer = optim.Adam(list(deep_kernel.parameters()) + list(gp_layer.parameters()), lr=0.01)

num_epochs = 100
# 모델을 학습
for epoch in range(num_epochs):
    optimizer.zero_grad()
    kernel_output = deep_kernel(x_tensor)
    predictive_mean, _ = gp_layer(kernel_output, y_tensor) # predictive_var는 사용 안함
    loss = loss_fn(predictive_mean, y_tensor)  # Use predictive_mean here
    loss.backward()
    optimizer.step()
    if(epoch % 10 == 0):
        print(f'Epoch {epoch+1}, Loss: {loss.item()}')

# 예측을 수행
with torch.no_grad():
    kernel_output = deep_kernel(x_tensor)
    predictive_mean, predictive_var = gp_layer(kernel_output, y_tensor)

# 결과를 시각화
sns.set()
plt.figure(figsize=(10, 6))
plt.plot(x, y, 'bo', label='Training Data')
plt.plot(x, predictive_mean.numpy(), 'r-', label='Predictive Mean')
plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
                 predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
                 alpha=0.2, label='95% CI')
plt.legend()
plt.show()

Epoch 1, Loss: 4.3467857893837725e-13
Epoch 11, Loss: 3.1288711313699757e-13
Epoch 21, Loss: 3.9212150236903054e-13
Epoch 31, Loss: 4.184870765894244e-13
Epoch 41, Loss: 2.9785689973499396e-13
Epoch 51, Loss: 3.8607078688482344e-13
Epoch 61, Loss: 3.9107123572454383e-13
Epoch 71, Loss: 2.359286811054462e-13
Epoch 81, Loss: 3.4729958167147024e-13
Epoch 91, Loss: 2.7600995490886793e-13

/tmp/ipykernel_1408185/2425174321.py:40: RuntimeWarning: invalid value encountered in sqrt
  plt.fill_between(x, predictive_mean.numpy() - 1.96 * np.sqrt(predictive_var.numpy().diagonal()),
/tmp/ipykernel_1408185/2425174321.py:41: RuntimeWarning: invalid value encountered in sqrt
  predictive_mean.numpy() + 1.96 * np.sqrt(predictive_var.numpy().diagonal()),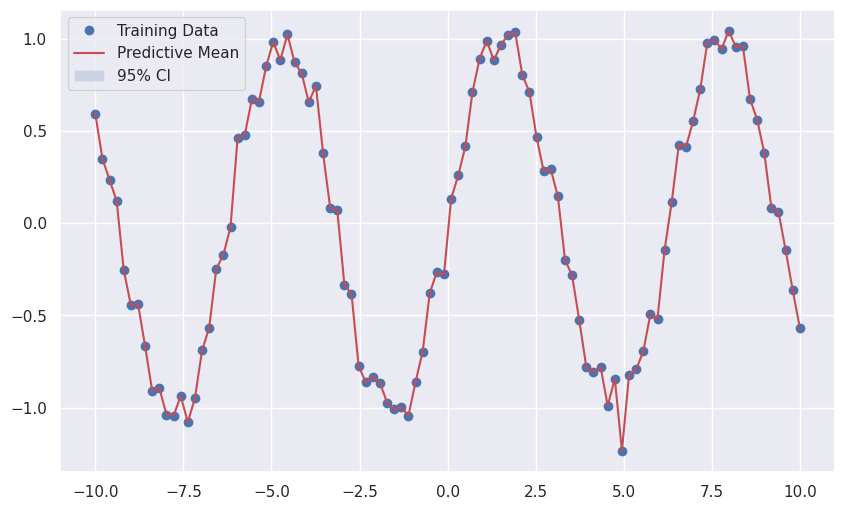

El aprendizaje del modelo utiliza la función de pérdida de error cuadrático medio (Mean Squared Error, MSE) y el optimizador Adam para aprender simultáneamente los parámetros de la red neuronal profunda y la capa GP.

6.6.4 Posibilidades y limitaciones del DKL

El ejemplo anterior muestra las ideas básicas detrás del aprendizaje de núcleos profundos (Deep Kernel Learning, DKL). Se utiliza un modelo de aprendizaje profundo (DeepKernel clase) para extraer características de los datos de entrada, y estas características se utilizan para calcular el kernel de un proceso gaussiano (GP). Luego, se usa el GP para calcular la media y la varianza (incertidumbre) de las predicciones. De esta manera, DKL combina la capacidad de aprendizaje representativo del aprendizaje profundo con la capacidad de estimación de incertidumbre del GP, lo que permite hacer predicciones confiables incluso en datos complejos.

Posibilidades del DKL:

• Eficiencia de datos: Los GPs tienden a funcionar bien incluso cuando los datos son escasos. DKL combina la potente capacidad de extracción de características del aprendizaje profundo con la eficiencia en datos del GP, lo que permite obtener un buen rendimiento incluso con pocos datos.
• Estimación de incertidumbre: DKL puede cuantificar la incertidumbre de las predicciones. Esto es muy útil en aplicaciones donde la seguridad es crucial (por ejemplo, diagnóstico médico, conducción autónoma).
• Flexibilidad: DKL se puede aplicar a diversos tipos de datos (imágenes, texto, gráficos, etc.). Se puede elegir libremente la arquitectura de la red neuronal para diseñar un extractor de características adecuado al problema.
• Combinación con optimización bayesiana: DKL se puede combinar con la optimización bayesiana para afinar eficientemente los hiperparámetros del modelo.

Limitaciones del DKL:

• Costo computacional: Los GPs siguen siendo costosos en términos de cálculo. En particular, a medida que aumenta el tamaño de los datos de entrenamiento, la matriz del kernel se hace más grande y el cálculo se vuelve más difícil.
• Diseño de redes neuronales: El rendimiento de DKL depende en gran medida del diseño del extractor de características (red neuronal). Elegir una arquitectura de red neuronal apropiada sigue siendo un problema complicado.
• Comprensión teórica insuficiente: El análisis teórico de DKL aún está en sus primeras etapas. Se necesitan más investigaciones para entender por qué DKL funciona bien y bajo qué condiciones muestra un buen rendimiento.

Conclusión

En este capítulo hemos examinado diversas técnicas para abordar el problema del sobreajuste en los modelos de aprendizaje profundo. El sobreajuste ocurre cuando un modelo de aprendizaje profundo se especializa excesivamente en los datos de entrenamiento y su rendimiento en la predicción de nuevos datos disminuye. Esto puede ocurrir cuando el modelo es demasiado complejo, hay pocos datos de entrenamiento, o los datos contienen mucho ruido. Prevenir el sobreajuste es una tarea crucial para aplicar modelos de aprendizaje profundo a problemas reales.

Las técnicas presentadas en este capítulo abordan el problema del sobreajuste de diferentes formas:

• Regularización: Se aplica una penalización a la complejidad del modelo para evitar que los pesos sean demasiado grandes. (L1, L2, Elastic Net)
• Dropout: Durante el entrenamiento, se eliminan aleatoriamente neuronas para evitar que el modelo dependa de neuronas o combinaciones específicas.
• Normalización por lotes: Se normalizan las entradas de cada capa para estabilizar y acelerar el aprendizaje.
• Optimización de hiperparámetros: Se utilizan métodos como la optimización bayesiana para encontrar combinaciones de hiperparámetros que optimicen el rendimiento del modelo.
• Procesos gaussianos, aprendizaje de núcleos profundos: Se modela explícitamente la incertidumbre para hacer predicciones más confiables. La combinación adecuada de estas técnicas y su ajuste según las características del problema es una de las habilidades más importantes de un ingeniero de deep learning. No existe una única solución “perfecta para todos los casos” y se debe buscar el mejor método a través de experimentación y análisis. La investigación en deep learning continúa avanzando rápidamente y es probable que surjan nuevas técnicas para abordar el sobreajuste.

Ejercicios de práctica

Problemas básicos

1. Explique los conceptos de sobreajuste (overfitting) y subajuste (underfitting), y describa cómo cada fenómeno afecta el rendimiento del modelo.
2. Explique las diferencias entre la regularización L1 y L2, y describa cómo cada tipo de regularización afecta los pesos del modelo.
3. Explique el principio de funcionamiento del dropout y cómo ayuda a prevenir el sobreajuste.
4. Explique el concepto de normalización por lotes (batch normalization) y describa qué beneficios proporciona para el entrenamiento de modelos de deep learning.
5. Describa los cambios en el gráfico mientras se modifican las funciones lambda en la función custom_loss dada.
6. Defina las normas L1 y L2.
7. Explique cómo se calculan la media y la varianza en la fórmula de normalización por lotes, y cómo estas se utilizan en el proceso de normalización.

Problemas aplicados

1. Entrene un modelo de regresión polinomial (polynomial regression) en un conjunto de datos dado y observe los fenómenos de sobreajuste y subajuste mientras varía el grado del polinomio. (Escriba código Python)
2. Cree un modelo de red neuronal simple, aplique regularización L1 o L2 y observe cómo cambian los pesos del modelo; compare los cambios en el rendimiento según la intensidad de la regularización. (Escriba código Python)
3. Entrene modelos de red neuronal con diferentes tasas de dropout y compare las pérdidas de entrenamiento/validación y la precisión para cada tasa. (Escriba código Python)
4. Compare la velocidad de aprendizaje y la estabilidad de convergencia del modelo de red neuronal mientras añade o elimina capas de normalización por lotes. (Escriba código Python)
5. Utilice el método de multiplicadores de Lagrange para derivar las condiciones óptimas de una función de pérdida con regularización L1 y L2 aplicadas.
6. Derive el proceso de retropropagación (backpropagation) en la normalización por lotes y explique cómo ayuda a mitigar el problema del desvanecimiento del gradiente.

Problemas avanzados

1. Visualice los efectos de la regularización L1 y L2 sobre la superficie de pérdida y explique el significado geométrico de cada tipo de regularización. (Escriba código Python)
2. Interprete el dropout desde la perspectiva del aprendizaje por ensamblaje (ensemble learning) y explique cómo se puede utilizar para estimar la incertidumbre del modelo.
3. Compare diferentes técnicas de optimización de hiperparámetros (búsqueda en cuadrícula, búsqueda aleatoria, optimización bayesiana, etc.) y describa las ventajas y desventajas de cada técnica.
4. Implemente la idea central de la optimización bayesiana para encontrar el valor óptimo de una función simple sin usar BoTorch. (Escriba código Python, se permite el uso de bibliotecas)
5. Explique los principios básicos del proceso gaussiano (Gaussian Process) y cómo realiza predicciones que incluyen incertidumbre.
6. Explique las condiciones que debe satisfacer la función kernel en un proceso gaussiano y demuestre que el kernel RBF satisface estas condiciones.
7. Explique el papel de la función de adquisición (acquisition function) en la optimización bayesiana, derive la fórmula de la función de adquisición Expected Improvement (EI) y explique su significado.

Haga clic para ver el contenido (soluciones de los ejercicios)

Soluciones de Ejercicios

Problemas Básicos

1. Sobreajuste/Subajuste:
   • Sobreajuste (Overfitting): El modelo se ajusta demasiado bien a los datos de entrenamiento, lo que resulta en un rendimiento (rendimiento de generalización) inferior en nuevos datos (datos de validación/prueba). Muestra un alto rendimiento en los datos de entrenamiento pero un bajo rendimiento en los datos de validación/prueba.
   • Subajuste (Underfitting): El modelo es demasiado simple y no logra aprender adecuadamente los patrones de los datos de entrenamiento. Muestra un bajo rendimiento en los datos de entrenamiento, validación y prueba.
2. Regularización L1/L2:
   • Regularización L1 (Lasso): Añade la suma de los valores absolutos de los pesos a la función de pérdida. \(\lambda \sum_{i} |w_i|\) Hace que algunos pesos sean exactamente 0, lo que tiene un efecto de selección de características (feature selection).
   • Regularización L2 (Ridge): Añade la suma de los cuadrados de los pesos a la función de pérdida. \(\lambda \sum_{i} (w_i)^2\) Reduce los pesos hacia 0, pero no los hace exactamente 0.
3. Dropout:
   • Principio de funcionamiento: Durante el proceso de entrenamiento, desactiva aleatoriamente algunos neuronas (hace que sus salidas sean 0).
   • Prevención del sobreajuste: Al aprender con diferentes combinaciones de neuronas cada vez, evita la dependencia en ciertas neuronas y produce un efecto de aprendizaje por ensamble.
4. Normalización por lotes:
   • Concepto: Normaliza las entradas de cada capa para que tengan una media de 0 y una varianza de 1.
   • Ventajas: Mejora la velocidad de entrenamiento, mitiga el problema del desvanecimiento/explosión del gradiente, permite el uso de tasas de aprendizaje más altas y tiene un efecto de regularización ligero.
5. Cambio de lambda en custom_loss:
   • Aumento de lambda: Aumenta la influencia del término de regularización. Los pesos se reducen, el modelo se simplifica y aumenta la posibilidad de subajuste.
   • Disminución de lambda: Reduce la influencia del término de regularización. Los pesos aumentan, el modelo se vuelve más complejo y aumenta la posibilidad de sobreajuste.
6. Normas L1/L2:
   • Norma L1: Suma de los valores absolutos de los elementos del vector. \(\| \mathbf{x} \|_1 = \sum_{i=1}^{n} |x_i|\)
   • Norma L2: Raíz cuadrada de la suma de los cuadrados de los elementos del vector. \(\| \mathbf{x} \|_2 = \sqrt{\sum_{i=1}^{n} x_i^2}\)
7. Normalización por lotes:
   • Media (μ): Media de las muestras dentro de un lote. \(\mu = \frac{1}{m} \sum_{i=1}^{m} x_i\)
   • Varianza (σ²): Varianza de las muestras dentro de un lote. \(\sigma^2 = \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu)^2\)
   • Normalización: \(x_{\text{norm}} = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}\) (ε es una pequeña constante para evitar la división por 0)

Problemas de Aplicación

1. Regresión Polinomial: (código omitido) Si el grado es demasiado alto, puede ocurrir sobreajuste; si es demasiado bajo, puede ocurrir subajuste.

2. Regularización L1/L2: (código omitido) Cuanto mayor sea la intensidad de regularización (lambda), más pequeños serán los pesos y se observarán cambios en el rendimiento.

3. Tasa de Dropout: (código omitido) Una tasa de dropout adecuada puede prevenir el sobreajuste y mejorar el rendimiento. Una tasa demasiado alta puede causar subajuste.

4. Normalización por lotes: (código omitido) Al agregar normalización por lotes, la velocidad de entrenamiento aumenta y tiende a converger de manera más estable.

5. Método de los multiplicadores de Lagrange:

   • Regularización L2: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_2^2 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + 2\lambda\mathbf{w} = 0\)
   • Regularización L1: \(L(\mathbf{w}, \lambda) = \text{Loss}(\mathbf{w}) + \lambda (\|\mathbf{w}\|_1 - c) \rightarrow \nabla_\mathbf{w}L = \nabla_\mathbf{w}\text{Loss}(\mathbf{w}) + \lambda \cdot \text{sign}(\mathbf{w}) = 0\) (sign(w) es el signo de w)

6. Retropropagación del batch normalization: (omitiendo la derivación) La normalización por lotes normaliza las entradas de cada capa para mitigar los problemas de desvanecimiento y explosión de gradientes, estabilizando así el aprendizaje.

Problemas avanzados

1. Visualización del plano de pérdida: (omitiendo el código) La regularización L1 genera restricciones en forma de rombo, mientras que la regularización L2 genera restricciones circulares, lo que resulta en soluciones óptimas formadas en diferentes ubicaciones.

2. Ensamblaje de dropout: El dropout tiene un efecto similar al aprendizaje por ensamblaje al entrenar con diferentes estructuras de red cada vez. Durante la predicción, se utilizan todos los neuronas (sin dropout) para realizar una predicción promedio. La incertidumbre de las predicciones puede estimarse mediante el dropout de Monte Carlo.

3. Técnicas de optimización de hiperparámetros:

   • Búsqueda en cuadrícula: Intenta todas las combinaciones posibles. Es muy costoso computacionalmente.
   • Búsqueda aleatoria: Prueba combinaciones aleatorias. Puede ser más eficiente que la búsqueda en cuadrícula.
   • Optimización bayesiana: Utiliza un modelo probabilístico basado en resultados previos de búsqueda para determinar el siguiente punto a explorar. Es eficiente.

4. Implementación de optimización bayesiana: (omitiendo el código) Se implementa utilizando un modelo sustituto (surrogate model, por ejemplo, proceso gaussiano) y una función de adquisición (acquisition function, por ejemplo, Expected Improvement).

5. Proceso gaussiano: Es una distribución de probabilidad sobre funciones. Utiliza una función kernel para definir la covarianza entre valores de función. Calcula la distribución a posteriori basada en datos observados, proporcionando la media y variancia (incertidumbre) de las predicciones.

6. Condiciones de la función kernel: Debe ser positiva semidefinida (positive semi-definite). La matriz kernel generada para cualquier conjunto de puntos de entrada debe ser una matriz positiva semidefinida (positive semi-definite matrix). El kernel RBF satisface esta condición. (omitiendo la prueba)

7. Función de adquisición: Se utiliza en optimización bayesiana para seleccionar el siguiente punto a explorar. Expected Improvement (EI) considera tanto la probabilidad de obtener un resultado mejor que el óptimo actual como la magnitud de esa mejora para seleccionar el próximo punto de exploración. (omitiendo la derivación de la fórmula)

1. Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): Artículo original que explica el concepto y efectos del dropout. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf)
2. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): Artículo original que explica el concepto y efectos de la normalización por lotes. (https://arxiv.org/abs/1502.03167)
3. Deep Learning (Goodfellow et al., 2016): Libro de texto sobre aprendizaje profundo. El capítulo 7 “Regularization for Deep Learning” trata detalladamente el tema del overfitting y las técnicas de regularización. (http://www.deeplearningbook.org/)
4. Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Explica las dificultades de entrenamiento en los modelos iniciales de aprendizaje profundo y la importancia de la inicialización de pesos. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf)
5. Regularization techniques for deep learning: A survey (Kukacka et al., 2017): Artículo que compara y analiza de manera integral diversas técnicas de regularización.
6. A Tutorial on Bayesian Optimization (Frazier, 2018): Tutorial que explica los conceptos básicos y aplicaciones de la optimización bayesiana. (https://arxiv.org/abs/1807.02811)
7. Bayesian Optimization (Garnett, 2023): Libro de texto completo sobre optimización bayesiana (https://www.bayesoptbook.com/)
8. Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): Libro de texto que aborda los principios básicos y aplicaciones en aprendizaje automático de los procesos gaussianos. (http://www.gaussianprocess.org/gpml/)
9. Deep Kernel Learning (Wilson et al., 2016): Artículo que explica el concepto y métodos del aprendizaje de kernels profundos. (https://arxiv.org/abs/1511.02222)
10. Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): Libro de texto práctico sobre aprendizaje automático y aprendizaje profundo. Explica el overfitting y las técnicas de regularización con ejemplos de código reales.
11. Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): Artículo sobre el optimizador Adam
12. Decoupled Weight Decay Regularization (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): Artículo sobre AdamW
13. Dropout: A Simple Way to Prevent Neural Networks from Overfitting (Srivastava et al., 2014): Artículo original que explica el concepto y los efectos del dropout. (https://www.cs.toronto.edu/~rsalakhu/papers/srivastava14a.pdf) 2. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (Ioffe & Szegedy, 2015): Artículo original que explica el concepto y los efectos de la normalización por lotes. (https://arxiv.org/abs/1502.03167) 3. Deep Learning (Goodfellow et al., 2016): Libro de texto de deep learning. El capítulo 7 “Regularization for Deep Learning” trata detalladamente el sobreajuste y las técnicas de regularización. (http://www.deeplearningbook.org/) 4. Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010): Explica las dificultades en el entrenamiento de modelos de deep learning iniciales y la importancia de los métodos de inicialización de pesos. (http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf) 5. Regularization techniques for deep learning: A survey (Kukacka et al., 2017): Artículo que compara y analiza de manera integral diversas técnicas de regularización. 6. A Tutorial on Bayesian Optimization (Frazier, 2018): Tutorial que explica los conceptos básicos y las aplicaciones de la optimización bayesiana. (https://arxiv.org/abs/1807.02811) 7. Bayesian Optimization (Garnett, 2023): Libro de texto integral sobre la optimización bayesiana (https://www.bayesoptbook.com/) 8. Gaussian Processes for Machine Learning (Rasmussen & Williams, 2006): Libro de texto que trata los principios básicos y las aplicaciones de machine learning de los procesos gaussianos. (http://www.gaussianprocess.org/gpml/) 9. Deep Kernel Learning (Wilson et al., 2016): Artículo que explica el concepto y los métodos del aprendizaje de núcleos profundos. (https://arxiv.org/abs/1511.02222) 10. Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow (Aurélien Géron, 2019): Libro de texto práctico sobre machine learning y deep learning. Explica el sobreajuste y las técnicas de regularización con ejemplos de código reales. 11. Adam: A Method for Stochastic Optimization (Kingma & Ba, 2014) (https://arxiv.org/abs/1412.6980): Artículo sobre el optimizador Adam 12. Decoupled Weight Decay Regularization (Loshchilov & Hutter, 2017) (https://arxiv.org/abs/1711.05101): Paper sobre AdamW

Traducción:

Título	Contenido
Ejemplo de texto	Este es un ejemplo de texto que debe traducirse, pero las expresiones matemáticas como \(E = mc^2\) y las tablas deben mantenerse intactas.